第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
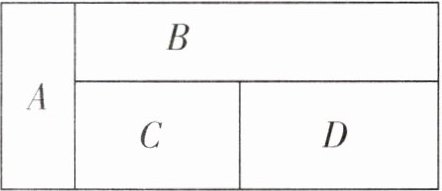
例 如图,把 A、B、C、D 四部分用红、黄、蓝、绿四种不同的颜色来涂,相邻的两部分不能使用同一种颜色。这幅图一共有多少种不同的涂色方法?
解析
给这幅图涂色要分为四步:
第一步给 A 涂色,可以任选一种颜色来涂,有 4 种涂法;
第二步给 B 涂色,由于 A、B 相邻,颜色不能相同,所以有 3 种涂色方法;
第三步给 C 涂色,由于 C 与 A、B 都相邻,所以只有 2 种涂色方法;
第四步给 D 涂色,D 与 B、C 两部分相邻,与 A 不相邻,所以也只有 2 种涂色方法。
答案:$4×3×2×2= 48$(种)
答:这幅图一共有 48 种不同的涂色方法。

解析
给这幅图涂色要分为四步:
第一步给 A 涂色,可以任选一种颜色来涂,有 4 种涂法;
第二步给 B 涂色,由于 A、B 相邻,颜色不能相同,所以有 3 种涂色方法;
第三步给 C 涂色,由于 C 与 A、B 都相邻,所以只有 2 种涂色方法;
第四步给 D 涂色,D 与 B、C 两部分相邻,与 A 不相邻,所以也只有 2 种涂色方法。
答案:$4×3×2×2= 48$(种)
答:这幅图一共有 48 种不同的涂色方法。
答案:
解析:
给这幅图涂色要分为四步:
第一步给A涂色,可以任选一种颜色来涂,有4种涂法;
第二步给B涂色,由于A、B相邻,颜色不能相同,所以有3种涂色方法;
第三步给C涂色,由于C与A、B都相邻,所以只有2种涂色方法;
第四步给D涂色,D与B、C两部分相邻,与A不相邻,所以也只有2种涂色方法。
答案:
$4×3×2×2 = 48$(种)
答:这幅图一共有48种不同的涂色方法。
给这幅图涂色要分为四步:
第一步给A涂色,可以任选一种颜色来涂,有4种涂法;
第二步给B涂色,由于A、B相邻,颜色不能相同,所以有3种涂色方法;
第三步给C涂色,由于C与A、B都相邻,所以只有2种涂色方法;
第四步给D涂色,D与B、C两部分相邻,与A不相邻,所以也只有2种涂色方法。
答案:
$4×3×2×2 = 48$(种)
答:这幅图一共有48种不同的涂色方法。
1. 用红、黄、黑、蓝、绿 5 种颜色给右下图中的A、B、C、D 四块区域涂色,要求每块区域用一种颜色且相邻区域的颜色不同。一共有多少种不同的涂色方法?


答案:
5×4×3×3 = 180(种)
【提示】给A涂色有5种方法;给B涂色时从剩下的4种颜色中选一种有4种方法;同理给C涂色时,与A、B区域的颜色不同,有3种方法;给D涂色有3种方法。
【提示】给A涂色有5种方法;给B涂色时从剩下的4种颜色中选一种有4种方法;同理给C涂色时,与A、B区域的颜色不同,有3种方法;给D涂色有3种方法。
2. 如右下图,平面上有 12 个点,可任意取其中四个点围成一个正方形,这样的正方形有多少个?


答案:
10个 【提示】把相邻的两点连接起来可以得到下面图形,从图中可以看出:
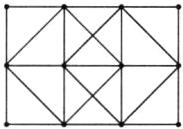
(1)最小的正方形有6个;
(2)由4个小正方形组合而成的正方形有2个;
(3)中间还可围成2个正方形。所以共有6 + 2 + 2 = 10(个)正方形。
10个 【提示】把相邻的两点连接起来可以得到下面图形,从图中可以看出:

(1)最小的正方形有6个;
(2)由4个小正方形组合而成的正方形有2个;
(3)中间还可围成2个正方形。所以共有6 + 2 + 2 = 10(个)正方形。
3. 甲、乙、丙、丁四人排成一列,要求甲在乙的前面(不一定相邻),一共有多少种不同的排法?
答案:
12种 【提示】根据题意,当甲排第一位时:甲乙丙丁、甲乙丁丙、甲丙乙丁、甲丙丁乙、甲丁乙丙、甲丁丙乙;当甲排第二位时:丁甲乙丙、丙甲乙丁、丁甲丙乙、丙甲丁乙;当甲排第三位时:丁丙甲乙、丙丁甲乙。一共有6 + 4 + 2 = 12(种)不同的排法。
4. 从 0、2、3、4 这四个数字中任意选取三个数字组成一个三位数,一共可以组成多少个不同的数?
答案:
18个 【提示】任意选取三个数字组合,因为0不能作为最高位,只能选择2、3、4作为最高位,然后分别列举出每个数字作为百位开头的有多少个。2开头的有234、243、203、230、204、240;3开头的有324、342、340、304、320、302;4开头的有423、432、403、430、402、420。
5. 如右下图,从上往下,沿线读出“努力学习好数学”。一共有多少种不同的路线?


答案:
20种 【提示】可作图如下。

20种 【提示】可作图如下。

查看更多完整答案,请扫码查看


