《2025年黄冈360定制课时六年级数学上册人教版》

1. 填一填。
(1)圆的周长= ( ),圆的面积= ( )。
(2)圆的周长和它的直径的比值是( ),它是一个( )小数,在计算时,一般只取它的近似值( )。
(3)圆有( )条对称轴,半圆有( )条对称轴。
(4)在一张长 10 厘米,宽 8 厘米的长方形纸上画一个最大的圆,圆的周长是( )厘米,面积是( )平方厘米。
(5)一个圆的周长扩大到原来的2倍,面积扩大到原来的( )倍。

答案： 1.
(1)$\pi d$(或$2\pi r$) $\pi r^{2}$
(2)$\pi$ 无限不循环 3.14
(3)无数 1
(4)25.12 50.24
(5)4
分析:
(4)在长10厘米,宽8厘米的长方形纸上画一个最大的圆,圆的直径是8厘米。圆的周长是$3.14×8=25.12$(厘米),面积是$3.14×(8÷2)^{2}=50.24$(平方厘米)。
(5)假设圆的周长是C,则圆的面积$=\pi×(\frac{C}{2\pi})^{2}=\frac{C^{2}}{4\pi}$。周长扩大到原来的2倍是2C,则圆的面积$=\frac{(2C)^{2}}{4\pi}=\frac{4C^{2}}{4\pi}$,面积扩大到原来的4倍。

2. 判断对错。
(1)圆环有无数条对称轴。( )
(2)一个整圆的面积总比半圆的面积大。( )
(3)扇形的面积总比圆的面积小。( )
(4)圆的周长等于$2\pi r$,所以半圆的周长是$\pi r$。( )

答案： 2.
(1)√
(2)×
(3)×
(4)×
分析:
(2)圆的半径未知,不能比较大小。
(3)圆的半径未知,不能比较扇形和圆面积的大小。
(4)半圆的周长是圆周长的一半($\pi r$)加一条直径的长度。

3. 求下列各图的周长和面积。

(1)
(2)

答案： 3.
(1)37.68 dm 113.04 dm²
(2)30.84 cm 56.52 cm²
分析:
(2)半圆的面积是圆面积的$\frac{1}{2}$,列式是$3.14×(12÷2)^{2}×\frac{1}{2}=56.52(cm^{2})$。
半圆的周长是圆周长的一半加一条直径的长度。列式是$3.14×12÷2+12=30.84(cm)$。

4. 绳子的长是10米,且绳子在树上可自由转动,牛能吃到草的最大面积是多少平方米?

答案： 4.$3.14×10^{2}=314$(平方米)
分析:牛能吃到草的最大面积是半径为10米的圆的面积。

5. 求下面各图形中阴影部分的面积。
(1)
(2)

答案： 5.
(1)50.24 cm²
(2)18.24 cm²

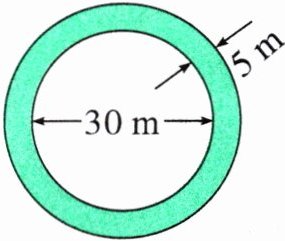
6. 一个圆形旱冰场的直径是30米,扩建后半径增加了5米。扩建后旱冰场的面积增加了多少平方米?

答案： 6.$30÷2=15(m)$
$15+5=20(m)$
$3.14×(20^{2}-15^{2})=549.5(m^{2})$
分析:扩建后旱冰场增加的面积是圆环的面积。内圆半径是$30÷2=15(m)$,外圆半径是$15+5=20(m)$,利用$S_{圆环}=S_{外圆}-S_{内圆}$计算出面积。

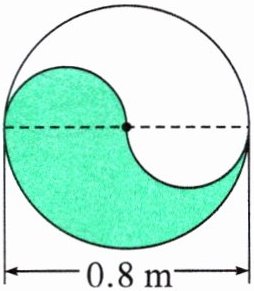
7. 涂色部分的周长和面积各是多少?

答案： 7.$0.8×3.14=2.512(m)$
$3.14×(\frac{0.8}{2})^{2}÷2=0.2512(m^{2})$
解析:把题图中2个小半圆组合成一个小圆。小圆的周长=大圆周长的$\frac{1}{2}$,即涂色部分周长等于大圆的周长。把上面小半圆补到下边空白处,涂色部分面积就是大圆面积的$\frac{1}{2}$。