第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 填一填。
(1)圆的周长除以( )的商是一个固定的数,通常把它叫作( ),用希腊字母( )表示,它是一个( )小数,计算时,通常保留两位小数,即( )。
(2)计算圆的周长时,已知 r,C= ( );已知 d,C= ( )。
(3)由 C= πd 可知,d= ( );
由 C= 2πr 可知,r= ( )。
(1)圆的周长除以( )的商是一个固定的数,通常把它叫作( ),用希腊字母( )表示,它是一个( )小数,计算时,通常保留两位小数,即( )。
(2)计算圆的周长时,已知 r,C= ( );已知 d,C= ( )。
(3)由 C= πd 可知,d= ( );
由 C= 2πr 可知,r= ( )。
答案:
1.
(1)直径 圆周率 π 无限不循环 3.14
(2)2πr πd
(3)$\frac{C}{\pi}$ $\frac{C}{2\pi}$ 提示:
(1)圆的周长与它的直径的比值是一个固定数,我们把它叫作圆周率,用字母 π 表示。它是一个无限不循环小数,实际应用中常取近似值 π≈3.14。
(1)直径 圆周率 π 无限不循环 3.14
(2)2πr πd
(3)$\frac{C}{\pi}$ $\frac{C}{2\pi}$ 提示:
(1)圆的周长与它的直径的比值是一个固定数,我们把它叫作圆周率,用字母 π 表示。它是一个无限不循环小数,实际应用中常取近似值 π≈3.14。
2. 判断对错。
(1)圆的周长是半径的 π 倍。 ( )
(2)圆周率 π= 3.14。 ( )
(3)圆的直径扩大到原来的 3 倍,周长也扩大到原来的 3 倍。 ( )
(4)大圆的圆周率比小圆的圆周率大。 ( )
(1)圆的周长是半径的 π 倍。 ( )
(2)圆周率 π= 3.14。 ( )
(3)圆的直径扩大到原来的 3 倍,周长也扩大到原来的 3 倍。 ( )
(4)大圆的圆周率比小圆的圆周率大。 ( )
答案:
2.
(1)×
(2)×
(3)√
(4)× 分析:
(1)圆周率不是圆的周长与它的半径的比值。因为直径是半径的 2 倍,所以周长与半径的比值为 2π。
(2)圆周率 π 是一个无限不循环小数,常取近似值 π≈3.14。
(3)周长 C=πd,π 是一个固定的数,直径 d 扩大到原来的 3 倍,周长也扩大到原来的 3 倍。
(4)圆周率是圆的周长与直径的比值,是一个固定的数,无论大圆、小圆,圆周率都相同。
(1)×
(2)×
(3)√
(4)× 分析:
(1)圆周率不是圆的周长与它的半径的比值。因为直径是半径的 2 倍,所以周长与半径的比值为 2π。
(2)圆周率 π 是一个无限不循环小数,常取近似值 π≈3.14。
(3)周长 C=πd,π 是一个固定的数,直径 d 扩大到原来的 3 倍,周长也扩大到原来的 3 倍。
(4)圆周率是圆的周长与直径的比值,是一个固定的数,无论大圆、小圆,圆周率都相同。
3. 选一选。
(1)甲圆的半径是乙圆半径的 3 倍,甲圆的周长是乙圆周长的( )倍。
A. 3
B. 6
C. 9
(2)车轮滚动一周走过的路程是车轮的( )。
A. 半径
B. 直径
C. 周长
(3)( )不能决定圆的大小。
A. 圆心
B. 圆的直径
C. 圆的周长
(4)小圆的直径和大圆的半径都是 6 cm,小圆周长是大圆周长的( )。
A. $\frac{1}{2}$
B. $\frac{1}{4}$
C. $\frac{1}{6}$
(1)甲圆的半径是乙圆半径的 3 倍,甲圆的周长是乙圆周长的( )倍。
A. 3
B. 6
C. 9
(2)车轮滚动一周走过的路程是车轮的( )。
A. 半径
B. 直径
C. 周长
(3)( )不能决定圆的大小。
A. 圆心
B. 圆的直径
C. 圆的周长
(4)小圆的直径和大圆的半径都是 6 cm,小圆周长是大圆周长的( )。
A. $\frac{1}{2}$
B. $\frac{1}{4}$
C. $\frac{1}{6}$
答案:
3.
(1)A
(2)C
(3)A
(4)A 分析:
(1)圆的周长 C=2πr,2π 是一个固定的数,甲圆的半径是乙圆半径的 3 倍,则甲圆周长是乙圆周长的 3 倍。
(3)圆心决定圆的位置。
(4)小圆直径和大圆的半径都是 6 cm,根据周长公式,小圆周长是 π×6=6π(cm),大圆周长是 2×π×6=12π(cm),(6π)÷(12π)=$\frac{1}{2}$,所以小圆的周长是大圆的$\frac{1}{2}$。
(1)A
(2)C
(3)A
(4)A 分析:
(1)圆的周长 C=2πr,2π 是一个固定的数,甲圆的半径是乙圆半径的 3 倍,则甲圆周长是乙圆周长的 3 倍。
(3)圆心决定圆的位置。
(4)小圆直径和大圆的半径都是 6 cm,根据周长公式,小圆周长是 π×6=6π(cm),大圆周长是 2×π×6=12π(cm),(6π)÷(12π)=$\frac{1}{2}$,所以小圆的周长是大圆的$\frac{1}{2}$。
4. 求下列各圆的周长。
(1)
(2)
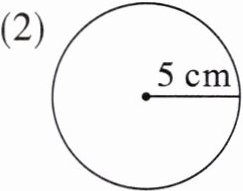
(1)

(2)

答案:
4.
(1)62.8 cm
(2)31.4 cm 提示:根据圆的周长公式 C=πd,C=2πr 进行计算,π≈3.14。
(1)62.8 cm
(2)31.4 cm 提示:根据圆的周长公式 C=πd,C=2πr 进行计算,π≈3.14。
5. 如右图:
(1)时针长 12 厘米,如果走 1 圈,它的尖端走过的路程是多少厘米?
(2)分针长 18 厘米,如果走 1 小时,它的尖端走过的路程是多少厘米?

(1)时针长 12 厘米,如果走 1 圈,它的尖端走过的路程是多少厘米?
(2)分针长 18 厘米,如果走 1 小时,它的尖端走过的路程是多少厘米?
答案:
5.
(1)2×3.14×12=75.36(厘米)
(2)2×3.14×18=113.04(厘米) 解析:
(1)时针走 1 圈,尖端走过的路程是圆的周长,时针长 12 厘米是圆的半径。根据周长公式 C=2πr 进行计算。
(2)分针走 1 小时,正好是 1 圈,尖端走过的路程是圆的周长。分针长 18 厘米是圆的半径,根据公式 C=2πr 计算。
(1)2×3.14×12=75.36(厘米)
(2)2×3.14×18=113.04(厘米) 解析:
(1)时针走 1 圈,尖端走过的路程是圆的周长,时针长 12 厘米是圆的半径。根据周长公式 C=2πr 进行计算。
(2)分针走 1 小时,正好是 1 圈,尖端走过的路程是圆的周长。分针长 18 厘米是圆的半径,根据公式 C=2πr 计算。
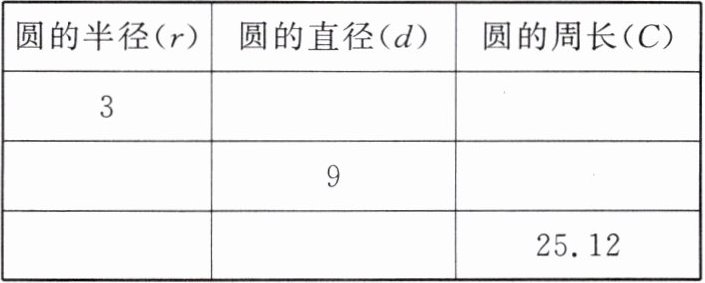
6. 将表格补充完整。(单位:dm)
| 圆的半径(r) | 圆的直径(d) | 圆的周长(C) |
| :----------: | :----------: | :----------: |
| 3 | | |
| | 9 | |
| | | 25.12 |
| 圆的半径(r) | 圆的直径(d) | 圆的周长(C) |
| :----------: | :----------: | :----------: |
| 3 | | |
| | 9 | |
| | | 25.12 |

答案:
6.6 18.84 4.5 28.26 4 8 提示:同一个圆中 d=2r,$r=\frac{1}{2}d$。根据周长公式 C=πd 或 C=2πr 计算周长。
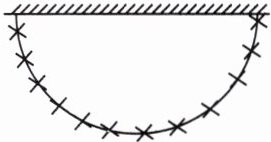
7. 如图,依墙而建的鸡舍呈半圆形,其直径为 5 米。在其四周围上篱笆(靠墙一面不围),需要多长的篱笆?

答案:
7.3.14×5÷2=7.85(米) 解析:由图知篱笆的长度就是圆周长的一半,列式为3.14×5÷2=7.85(米)。
查看更多完整答案,请扫码查看


