《2025年亮点给力提优班六年级数学上册苏教版》

1. (1) 做一节长2米,横截面是边长为4分米的正方形的铁皮通风管,至少要用3.2平方米的铁皮。

答案： 3.2

(2) 张伯伯要在墙角搭一个正方体形状的鸡笼(两面靠墙)。搭鸡笼用的3根框架共用去钢筋12米(如图),如果露在外面的面用塑料网包裹,那么至少需要(48)平方米的塑料网。

答案： 48

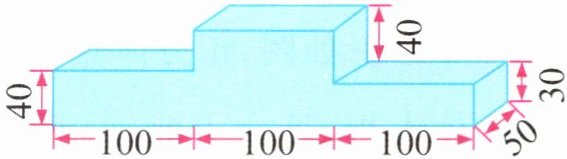
(3) 下图是运动会的领奖台(单位:cm),要求除底面不涂漆外,其他各面都涂漆。需要涂漆的面积是(5)$m^{2}$。

答案： 5

2. 学校科技馆大门前有5级台阶,每级台阶等高等宽(如图),在这些台阶面上(涂色部分)铺上地毯,至少需要多少平方米的地毯?

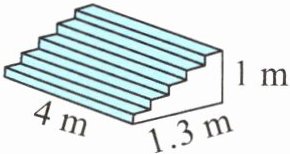
答案： 4×1.3+4×1=9.2(平方米)

3. 如图是体育课用的可以折叠的垫子,折叠前后的形状都是长方体。制作一个这样的垫子至少需要多少平方米帆布?

答案： 5分米=0.5米 20厘米=0.2米 0.2÷2=0.1(米) 0.5×0.5×2+0.5×0.1×4=0.7(平方米) 0.7×2=1.4(平方米)

4. 新趋势 推导探究 下面两个立体图形都是由棱长1厘米的正方体搭成的。

立体图形①的表面积$=(4+7+6)×2= 34$(平方厘米),其中4平方厘米、7平方厘米、6平方厘米分别是从上面、前面和右面看到的图形的面积。
(1) 用求立体图形①的表面积的方法,求立体图形②的表面积,列式为(9+7+7)×2。
(2) 若添加同样大的正方体,把立体图形②补成一个长方体,则这个长方体的表面积至少是66平方厘米。

答案： （1）(9+7+7)×2 （2）66

5. 一个长方体的长是5分米,宽是2分米,高是3分米。如果要使这个长方体的表面积增加20平方分米,宽和高都不变,那么长应增加(2)分米。

答案： 2

6. 把一个正方体木块锯成两个大小不同的长方体,其中小长方体的表面积比大长方体的表面积少20平方厘米,原来正方体木块的棱长是5厘米,小长方体的表面积是多少平方厘米?

答案： (5×5×8-20)÷2=90(平方厘米) 解析 把正方体木块锯成两个大小不同的长方体,增加了2个面,两个长方体的表面积之和相当于正方体的8个面的面积和,即5×5×8=200(平方厘米)。由于小长方体的表面积比大长方体的表面积少20平方厘米,根据差问题的求法可以求出小长方体的表面积。