第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
例1 如图,把4个完全一样的正方体拼成一个长方体,这个长方体的表面积是540平方厘米,原来一个正方体的表面积是多少平方厘米?

思路分析

规范解答 $6×4 - 2×(4 - 1) = 18$(个)
$540÷18×6 = 180$(平方厘米)
答:原来一个正方体的表面积是180平方厘米。

思路分析

规范解答 $6×4 - 2×(4 - 1) = 18$(个)
$540÷18×6 = 180$(平方厘米)
答:原来一个正方体的表面积是180平方厘米。
答案:
解析:
本题考查了长方体和正方体表面积的计算。
通过观察可知,把$4$个完全一样的正方体拼成一个长方体,有$6$个面重合,所以长方体的表面积比$4$个正方体的表面积之和减少了$6$个小正方形的面积,由此求出正方体一个面的面积,进而求出一个正方体的表面积。
答案:
$6×4 - 2×(4 - 1) = 18$(个)
$540÷18×6 = 180$(平方厘米)
答:原来一个正方体的表面积是$180$平方厘米。
本题考查了长方体和正方体表面积的计算。
通过观察可知,把$4$个完全一样的正方体拼成一个长方体,有$6$个面重合,所以长方体的表面积比$4$个正方体的表面积之和减少了$6$个小正方形的面积,由此求出正方体一个面的面积,进而求出一个正方体的表面积。
答案:
$6×4 - 2×(4 - 1) = 18$(个)
$540÷18×6 = 180$(平方厘米)
答:原来一个正方体的表面积是$180$平方厘米。
一根长方体方钢长2米,将它截成三段后,表面积增加了32平方分米。原来这根长方体方钢的体积是(
160
)立方分米。
答案:
160
跟踪练习2 如图,将若干个相同的小正方体叠成一个长方体,这个长方体的底面就是原正方体的底面。整个长方体的表面积是650平方厘米,当从这个长方体的顶部拿去一个正方体后,新长方体的表面积比原来减少100平方厘米。原长方体由多少个小正方体拼成?
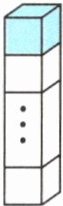

答案:
100÷4=25(平方厘米)
解:设原长方体由a个小正方体拼成。
(4a+2)×25=650 a=6
解:设原长方体由a个小正方体拼成。
(4a+2)×25=650 a=6
例2 小枫放学回家,看见桌上放着两个玻璃鱼缸,爸爸在留言条上写着:“小枫,你回家后,把A鱼缸的水倒一些到B鱼缸中,使两个鱼缸中的水深一样。”小枫按留言条倒水后,这两个鱼缸现在的水深是多少厘米?(鱼缸壁厚度忽略不计)

思路分析 方法一:不管怎么倒水,水的体积不变。可以将两个鱼缸并排放在一起,将有水的部分看成是一个长$(20 + 40)$厘米、宽50厘米的长方体(如图)。由“长方体的体积= 底面积×高”可知,“长方体的高= 体积÷底面积”,从而计算出现在的水深。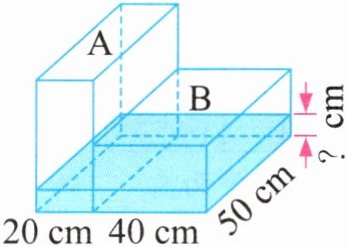
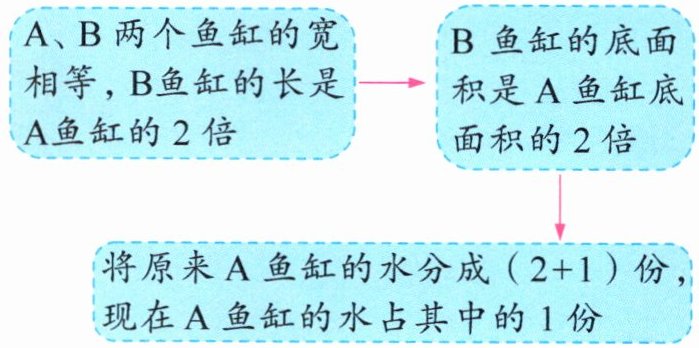
方法二:
规范解答 方法一:$20×50×24÷[(20 + 40)×50] = 8$(厘米)
方法二:$24÷(40÷20 + 1) = 8$(厘米)
答:这两个鱼缸现在的水深是8厘米。

思路分析 方法一:不管怎么倒水,水的体积不变。可以将两个鱼缸并排放在一起,将有水的部分看成是一个长$(20 + 40)$厘米、宽50厘米的长方体(如图)。由“长方体的体积= 底面积×高”可知,“长方体的高= 体积÷底面积”,从而计算出现在的水深。

方法二:

规范解答 方法一:$20×50×24÷[(20 + 40)×50] = 8$(厘米)
方法二:$24÷(40÷20 + 1) = 8$(厘米)
答:这两个鱼缸现在的水深是8厘米。
答案:
解析:本题考查利用长方体体积公式解决实际问题,关键在于抓住水的体积不变这一条件。
方法一是将两个鱼缸并排看作一个大的长方体,根据长方体体积公式先求出总体积,再除以新的底面积得到水深;
方法二是根据两个鱼缸底面积的倍数关系,将原来$A$鱼缸的水进行份数划分来计算现在的水深。
答案:
方法一:
$20×50×24÷[(20 + 40)×50]$
$=20×50×24÷(60×50)$
$=24000÷3000$
$= 8$(厘米)
方法二:
$24÷(40÷20 + 1)$
$=24÷(2 + 1)$
$=24÷3$
$= 8$(厘米)
答:这两个鱼缸现在的水深是$8$厘米。
方法一是将两个鱼缸并排看作一个大的长方体,根据长方体体积公式先求出总体积,再除以新的底面积得到水深;
方法二是根据两个鱼缸底面积的倍数关系,将原来$A$鱼缸的水进行份数划分来计算现在的水深。
答案:
方法一:
$20×50×24÷[(20 + 40)×50]$
$=20×50×24÷(60×50)$
$=24000÷3000$
$= 8$(厘米)
方法二:
$24÷(40÷20 + 1)$
$=24÷(2 + 1)$
$=24÷3$
$= 8$(厘米)
答:这两个鱼缸现在的水深是$8$厘米。
跟踪练习3 如图,有一块长方形地,甲处比乙处高50厘米。现在要把这块地推平整,使得甲、乙两处一样高,要从甲处推下多少厘米厚的土填在乙处?


答案:
50厘米=0.5米 (100-40)×30×0.5÷(100×30)=0.3(米) 0.5-0.3=0.2(米) 0.2米=20厘米
查看更多完整答案,请扫码查看


