第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
例3 从一个棱长10厘米的正方体木块上平行于某条棱挖去一个长10厘米、宽2厘米、高2厘米的小长方体,剩下部分的表面积是多少平方厘米?
思路分析 本题有多种情况:
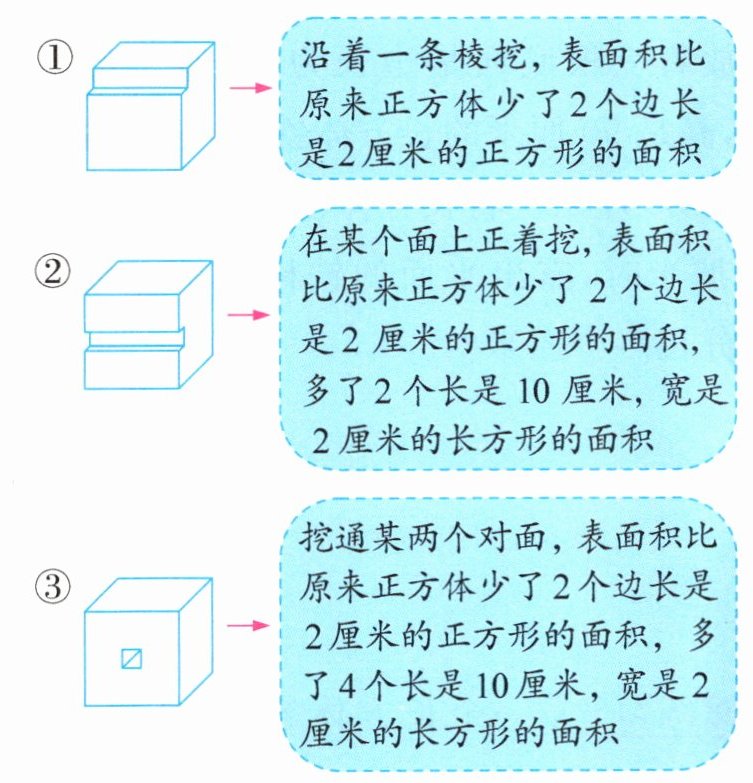
规范解答 情况一:$10×10×6 - 2×2×2 = 592$(平方厘米)
情况二:$10×10×6 - 2×2×2 + 10×2×2 = 632$(平方厘米)
情况三:$10×10×6 - 2×2×2 + 10×2×4 = 672$(平方厘米)
答:剩下部分的表面积可能是592平方厘米或632平方厘米或672平方厘米。
思路分析 本题有多种情况:

规范解答 情况一:$10×10×6 - 2×2×2 = 592$(平方厘米)
情况二:$10×10×6 - 2×2×2 + 10×2×2 = 632$(平方厘米)
情况三:$10×10×6 - 2×2×2 + 10×2×4 = 672$(平方厘米)
答:剩下部分的表面积可能是592平方厘米或632平方厘米或672平方厘米。
答案:
解析:本题考查正方体挖去一个长方体后表面积的变化情况,需要根据不同的挖法,分析表面积的变化,进而计算出剩下部分的表面积。
情况一:沿着一条棱挖,表面积减少$2$个边长为$2$厘米的正方形的面积。
情况二:在某个面上正着挖,表面积减少$2$个边长为$2$厘米的正方形的面积,同时增加了$2$个长是$10$厘米、宽是$2$厘米的长方形的面积。
情况三:挖通某两个对面,表面积减少$2$个边长为$2$厘米的正方形的面积,同时增加了$4$个长是$10$厘米、宽是$2$厘米的长方形的面积。
答案:原正方体表面积:$10×10×6 = 600$(平方厘米)
情况一:
减少的面积:$2×2×2 = 8$(平方厘米)
剩下部分表面积:$600 - 8 = 592$(平方厘米)
情况二:
减少的面积:$2×2×2 = 8$(平方厘米)
增加的面积:$10×2×2 = 40$(平方厘米)
剩下部分表面积:$600 - 8 + 40 = 632$(平方厘米)
情况三:
减少的面积:$2×2×2 = 8$(平方厘米)
增加的面积:$10×2×4 = 80$(平方厘米)
剩下部分表面积:$600 - 8 + 80 = 672$(平方厘米)
答:剩下部分的表面积可能是$592$平方厘米或$632$平方厘米或$672$平方厘米。
情况一:沿着一条棱挖,表面积减少$2$个边长为$2$厘米的正方形的面积。
情况二:在某个面上正着挖,表面积减少$2$个边长为$2$厘米的正方形的面积,同时增加了$2$个长是$10$厘米、宽是$2$厘米的长方形的面积。
情况三:挖通某两个对面,表面积减少$2$个边长为$2$厘米的正方形的面积,同时增加了$4$个长是$10$厘米、宽是$2$厘米的长方形的面积。
答案:原正方体表面积:$10×10×6 = 600$(平方厘米)
情况一:
减少的面积:$2×2×2 = 8$(平方厘米)
剩下部分表面积:$600 - 8 = 592$(平方厘米)
情况二:
减少的面积:$2×2×2 = 8$(平方厘米)
增加的面积:$10×2×2 = 40$(平方厘米)
剩下部分表面积:$600 - 8 + 40 = 632$(平方厘米)
情况三:
减少的面积:$2×2×2 = 8$(平方厘米)
增加的面积:$10×2×4 = 80$(平方厘米)
剩下部分表面积:$600 - 8 + 80 = 672$(平方厘米)
答:剩下部分的表面积可能是$592$平方厘米或$632$平方厘米或$672$平方厘米。
跟踪练习4 用橡皮泥做一个棱长为5厘米的正方体,先在上面中心位置处从上到下打一个边长为1厘米的正方形通孔,如图①,再在正面中心位置处从前到后打一个边长为1厘米的正方形通孔,如图②。打孔后橡皮泥的体积是多少立方厘米?打孔后橡皮泥的表面积是多少平方厘米?
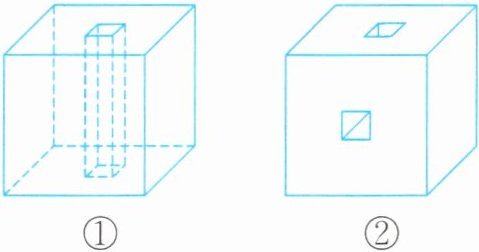

答案:
5×5×5-1×1×5×2+1×1×1=116(立方厘米) 5×5×6-1×1×4+1×(5-1)×4×2+1×1×2=180(平方厘米)
例4 一种蜡笔盒长和宽都是8厘米,高是3厘米,乐乐想把6个这样的蜡笔盒包装成一个长方体,怎样包最省包装纸?请你算一算,最少需要多少平方厘米的包装纸?(包装纸的重叠部分忽略不计)
思路分析 要想最省包装纸,则尽量将较大的面拼接在一起。$6 = 1×1×6 = 1×2×3$,三种较为节省包装纸的包装方法如下图。

分别计算三种包装方法的表面积后比较即可。
规范解答 包法一:$3×6 = 18$(厘米) $8×8×2 + 8×18×4 = 704$(平方厘米)
包法二:$8×2 = 16$(厘米) $3×3 = 9$(厘米) $(8×16 + 8×9 + 16×9)×2 = 688$(平方厘米)
包法三:$8×3 = 24$(厘米) $3×2 = 6$(厘米) $(8×24 + 8×6 + 24×6)×2 = 768$(平方厘米)
$688 < 704 < 768$
答:包装成长16厘米、宽8厘米、高9厘米的长方体最节省包装纸,最少需要688平方厘米的包装纸。
思路分析 要想最省包装纸,则尽量将较大的面拼接在一起。$6 = 1×1×6 = 1×2×3$,三种较为节省包装纸的包装方法如下图。

分别计算三种包装方法的表面积后比较即可。
规范解答 包法一:$3×6 = 18$(厘米) $8×8×2 + 8×18×4 = 704$(平方厘米)
包法二:$8×2 = 16$(厘米) $3×3 = 9$(厘米) $(8×16 + 8×9 + 16×9)×2 = 688$(平方厘米)
包法三:$8×3 = 24$(厘米) $3×2 = 6$(厘米) $(8×24 + 8×6 + 24×6)×2 = 768$(平方厘米)
$688 < 704 < 768$
答:包装成长16厘米、宽8厘米、高9厘米的长方体最节省包装纸,最少需要688平方厘米的包装纸。
答案:
解析:本题考查长方体表面积的计算及最优化问题。
把6个棱长为8厘米、8厘米、3厘米的长方体蜡笔盒包装成一个长方体,要想最省包装纸,则尽量将较大的面拼接在一起。
先找出6的因数分解方式,即$6 = 1×1×6 = 1×2×3$,对应三种包装方法,分别计算三种包装方法的表面积后比较大小,表面积最小的即为最省包装纸的包装方法。
答案:包法一:把6个蜡笔盒叠摞在一起,此时新长方体的长、宽不变,高变为$3×6 = 18$(厘米)。
根据长方体表面积公式$S=(ab + ah + bh)×2$(其中$a$为长,$b$为宽,$h$为高),可得其表面积为$8×8×2 + 8×18×4 = 128 + 576 = 704$(平方厘米)。
包法二:将6个蜡笔盒排成2层,每层3个,此时新长方体的长不变,宽变为$8×2 = 16$(厘米),高变为$3×3 = 9$(厘米),其表面积为$(8×16 + 8×9 + 16×9)×2 = (128 + 72 + 144)×2 = 344×2 = 688$(平方厘米)。
包法三:将6个蜡笔盒排成2排,每排3个,此时新长方体的长变为$8×3 = 24$(厘米),宽变为$3×2 = 6$(厘米),高不变,其表面积为$(8×24 + 8×6 + 24×6)×2 = (192 + 48 + 144)×2 = 384×2 = 768$(平方厘米)。
因为$688<704<768$,
所以包装成长16厘米、宽8厘米、高9厘米的长方体最节省包装纸,最少需要688平方厘米的包装纸。
把6个棱长为8厘米、8厘米、3厘米的长方体蜡笔盒包装成一个长方体,要想最省包装纸,则尽量将较大的面拼接在一起。
先找出6的因数分解方式,即$6 = 1×1×6 = 1×2×3$,对应三种包装方法,分别计算三种包装方法的表面积后比较大小,表面积最小的即为最省包装纸的包装方法。
答案:包法一:把6个蜡笔盒叠摞在一起,此时新长方体的长、宽不变,高变为$3×6 = 18$(厘米)。
根据长方体表面积公式$S=(ab + ah + bh)×2$(其中$a$为长,$b$为宽,$h$为高),可得其表面积为$8×8×2 + 8×18×4 = 128 + 576 = 704$(平方厘米)。
包法二:将6个蜡笔盒排成2层,每层3个,此时新长方体的长不变,宽变为$8×2 = 16$(厘米),高变为$3×3 = 9$(厘米),其表面积为$(8×16 + 8×9 + 16×9)×2 = (128 + 72 + 144)×2 = 344×2 = 688$(平方厘米)。
包法三:将6个蜡笔盒排成2排,每排3个,此时新长方体的长变为$8×3 = 24$(厘米),宽变为$3×2 = 6$(厘米),高不变,其表面积为$(8×24 + 8×6 + 24×6)×2 = (192 + 48 + 144)×2 = 384×2 = 768$(平方厘米)。
因为$688<704<768$,
所以包装成长16厘米、宽8厘米、高9厘米的长方体最节省包装纸,最少需要688平方厘米的包装纸。
查看更多完整答案,请扫码查看


