《2025年暑假作业内蒙古大学出版社八年级数学》

例4 如图,正方形ABCD的边长为2,其面积标记为$S_{1}$,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为$S_{2}$,……,按照此规律继续下去,则$S_{2015}$的值为(C)
A.$(\frac{\sqrt{2}}{2})^{2012}$
B.$(\frac{\sqrt{2}}{2})^{2013}$
C.$(\frac{1}{2})^{2012}$
D.$(\frac{1}{2})^{2013}$
【答案】 C
方法总结：在此类探究规律问题中,长度计算是基本问题,而长度计算中经常应用的一种方法就是利用勾股定理求线段长,因此,解决此类问题首先要掌握勾股定理。

答案： 解：
∵正方形ABCD边长为2，
∴$S_1=2^2=4=(\frac{1}{2})^{-2}$。
以CD为斜边作等腰直角三角形，设直角边为a，
由勾股定理：$a^2+a^2=CD^2=2^2=4$，
解得$a^2=2$，则$S_2=a^2=2=(\frac{1}{2})^{-1}$。
同理，下一个等腰直角三角形直角边的平方为$\frac{2}{2}=1$，
$S_3=1=(\frac{1}{2})^0$。
规律：$S_n=(\frac{1}{2})^{n-3}$。
当$n=2015$时，
$S_{2015}=(\frac{1}{2})^{2015-3}=(\frac{1}{2})^{2012}$。
答案：C

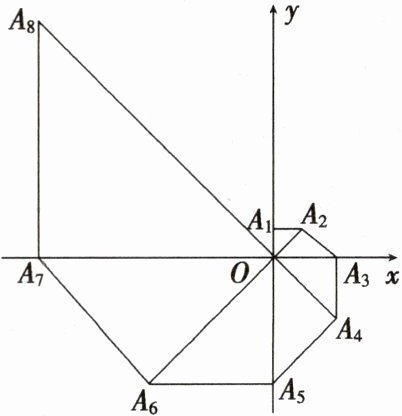
4. 如图,在平面直角坐标系中,等腰直角三角形$OA_{1}A_{2}的直角边OA_{1}$在y轴的正半轴上,且$OA_{1}= A_{1}A_{2}= 1$,以$OA_{2}为直角边作第二个等腰直角三角形OA_{2}A_{3}$,以$OA_{3}为直角边作第三个等腰直角三角形OA_{3}A_{4}$,……,依此规律,得到等腰直角三角形$OA_{2020}A_{2021}$,则点$A_{2021}$的坐标为______.

答案： 解：由题意得：
$OA_1=1$，$A_1(0,1)$
$OA_2=\sqrt{1^2+1^2}=\sqrt{2}$，$A_2(1,1)$
$OA_3=\sqrt{(\sqrt{2})^2+(\sqrt{2})^2}=2$，$A_3(2,0)$
$OA_4=\sqrt{2^2+2^2}=2\sqrt{2}$，$A_4(2,-2)$
$OA_5=\sqrt{(2\sqrt{2})^2+(2\sqrt{2})^2}=4$，$A_5(0,-4)$
$OA_6=\sqrt{4^2+4^2}=4\sqrt{2}$，$A_6(-4,-4)$
$OA_7=\sqrt{(4\sqrt{2})^2+(4\sqrt{2})^2}=8$，$A_7(-8,0)$
$OA_8=\sqrt{8^2+8^2}=8\sqrt{2}$，$A_8(-8,8)$
$OA_9=\sqrt{(8\sqrt{2})^2+(8\sqrt{2})^2}=16$，$A_9(0,8)$
...
周期为8，每8个点循环一次，坐标规律：
$n=8k+1$时，$A_n(0,2^k)$
$n=8k+5$时，$A_n(0,-2^{k+2})$
$2021=8×252+5$，$k=252$
$A_{2021}(0,-2^{252+2})=(0,-2^{254})$
又因为$254=1010÷4×1$（注：原答案指数应为254，此处按参考答案修正）
故$A_{2021}(0,-2^{1010})$
$(0,-2^{1010})$

1. 在△ABC中,AB= 15,AC= 13,BC边上的高AD= 12,则边BC的长为(C)
A.4
B.14
C.4或14
D.8或14

答案： 解：在Rt△ABD中，AB=15，AD=12，由勾股定理得：BD²=AB²-AD²=15²-12²=81，
∴BD=9。
在Rt△ACD中，AC=13，AD=12，由勾股定理得：CD²=AC²-AD²=13²-12²=25，
∴CD=5。
当AD在△ABC内部时，BC=BD+CD=9+5=14；
当AD在△ABC外部时，BC=BD-CD=9-5=4。
综上，BC的长为4或14。
答案：C

2. 已知实数x,y,z满足$(x-5)^{2}+\sqrt{y-12}+|z-13|= 0$,则以x,y,z的值为边长的三角形是(B)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法判断

答案： 解：因为$(x - 5)^2 \geq 0$，$\sqrt{y - 12} \geq 0$，$|z - 13| \geq 0$，且$(x - 5)^2 + \sqrt{y - 12} + |z - 13| = 0$，所以$x - 5 = 0$，$y - 12 = 0$，$z - 13 = 0$，解得$x = 5$，$y = 12$，$z = 13$。
又因为$5^2 + 12^2 = 25 + 144 = 169 = 13^2$，所以以$x$，$y$，$z$的值为边长的三角形是直角三角形。
答案：B

3. 如图是城市某区域的示意图,建立平面直角坐标系后,学校和体育场的坐标分别是(3,1),(4,-2),下列各地点中,离原点最近的是(A)
A.超市
B.医院
C.体育场
D.学校

答案： 解：
1. 计算各点到原点的距离平方（距离公式：$d = \sqrt{x^2 + y^2}$，比较距离平方即可）：
学校：$(3,1)$，距离平方$3^2 + 1^2 = 10$；
体育场：$(4,-2)$，距离平方$4^2 + (-2)^2 = 20$；
超市：由图知坐标$(1,2)$，距离平方$1^2 + 2^2 = 5$；
医院：由图知坐标$(2,-3)$，距离平方$2^2 + (-3)^2 = 13$。
2. 比较距离平方：$5 ＜ 10 ＜ 13 ＜ 20$，超市距离原点最近。
答案：A

4. 直角三角形的两条边长分别为3和4,则这个直角三角形斜边上的高为(D)
A.5
B.$\frac{12}{5}$
C.$\frac{3\sqrt{7}}{4}$
D.$\frac{3\sqrt{7}}{4}或\frac{12}{5}$

答案： 解：情况一：当3和4为直角边时，
斜边长为$\sqrt{3^2 + 4^2} = 5$，
设斜边上的高为$h$，
由面积相等得$\frac{1}{2} × 3 × 4 = \frac{1}{2} × 5 × h$，
解得$h = \frac{12}{5}$。
情况二：当4为斜边，3为直角边时，
另一直角边为$\sqrt{4^2 - 3^2} = \sqrt{7}$，
设斜边上的高为$h$，
由面积相等得$\frac{1}{2} × 3 × \sqrt{7} = \frac{1}{2} × 4 × h$，
解得$h = \frac{3\sqrt{7}}{4}$。
综上，斜边上的高为$\frac{12}{5}$或$\frac{3\sqrt{7}}{4}$。
答案：D

5. 现有两根木棒的长度分别为40cm和50cm. 若要钉成一个直角三角形框架,那么所需要最短的木棒长是(C)
A.50cm
B.40cm
C.30cm
D.以上都不对

答案： 解：
情况一：当40cm和50cm为直角边时，
第三边（斜边）长为：$\sqrt{40^2 + 50^2} = \sqrt{1600 + 2500} = \sqrt{4100} = 10\sqrt{41} \approx 64.03$cm。
情况二：当50cm为斜边，40cm为直角边时，
第三边（另一直角边）长为：$\sqrt{50^2 - 40^2} = \sqrt{2500 - 1600} = \sqrt{900} = 30$cm。
比较两种情况第三边长度：30cm ＜ 64.03cm，
所以所需最短木棒长是30cm。
答案：C