《2025年暑假作业内蒙古大学出版社八年级数学》

23. 如图所示,在$\triangle ABC$中,点D,E分别为AB,AC的中点,点H在线段CE上,连接BH,点G,F分别为BH,CH的中点.

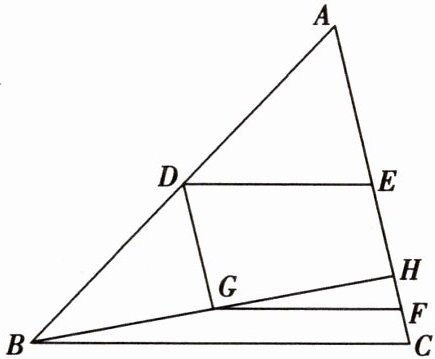
(1)求证：四边形DEFG为平行四边形；
(2)$DG⊥BH$,$BD= 3$,$EF= 2$,求线段BG的长度.

答案：
(1) 证明：
∵点D，E分别为AB，AC的中点，
∴DE是△ABC的中位线，
∴DE//BC，DE=$\frac{1}{2}$BC。
∵点G，F分别为BH，CH的中点，
∴GF是△HBC的中位线，
∴GF//BC，GF=$\frac{1}{2}$BC，
∴DE//GF，DE=GF，
∴四边形DEFG为平行四边形。
(2) 解：
∵四边形DEFG为平行四边形，
∴DG=EF=2。
∵DG⊥BH，
∴∠DGB=90°。
在Rt△DGB中，BD=3，DG=2，
∴BG=$\sqrt{BD^2 - DG^2}=\sqrt{3^2 - 2^2}=\sqrt{5}$。
即线段BG的长度为$\sqrt{5}$。

24. 如图,D,E,F分别是$\triangle ABC$各边的中点,连接DE,EF,AE.
(1)求证：四边形ADEF为平行四边形；
(2)加上条件②（或③）后,能使得四边形ADEF为菱形,请从①$∠BAC= 90^{\circ }$；②AE平分$∠BAC$；③$AB= AC$这3个条件中选择1个条件填空(写序号),并加以证明.
(1) 证明：
∵ D，E，F 分别是△ABC 各边的中点，
∴ DE 是△ABC 的中位线，EF 是△ABC 的中位线，
∴ DE//AC，DE = 1/2 AC，EF//AB，EF = 1/2 AB，
∵ F 是 AC 的中点，∴ AF = 1/2 AC，
∴ DE//AF 且 DE = AF，
∴ 四边形 ADEF 为平行四边形。
(2) 证明（选②）：
∵ AE 平分∠BAC，∴ ∠DAE = ∠FAE，
∵ 四边形 ADEF 为平行四边形，∴ EF//AD，
∴ ∠AEF = ∠DAE，
∴ ∠AEF = ∠FAE，
∴ AF = EF，
∴ 平行四边形 ADEF 为菱形。
证明（选③）：
∵ AB = AC，EF = 1/2 AB，DE = 1/2 AC，
∴ EF = DE，
∴ 平行四边形 ADEF 为菱形。

答案：
(1) 证明：
∵ D，E，F 分别是△ABC 各边的中点，
∴ DE 是△ABC 的中位线，EF 是△ABC 的中位线，
∴ DE//AC，DE = 1/2 AC，EF//AB，EF = 1/2 AB，
∵ F 是 AC 的中点，
∴ AF = 1/2 AC，
∴ DE//AF 且 DE = AF，
∴ 四边形 ADEF 为平行四边形。
(2) ②（或③）
证明（选②）：
∵ AE 平分∠BAC，
∴ ∠DAE = ∠FAE，
∵ 四边形 ADEF 为平行四边形，
∴ EF//AD，
∴ ∠AEF = ∠DAE，
∴ ∠AEF = ∠FAE，
∴ AF = EF，
∴ 平行四边形 ADEF 为菱形。
证明（选③）：
∵ AB = AC，EF = 1/2 AB，DE = 1/2 AC，
∴ EF = DE，
∴ 平行四边形 ADEF 为菱形。

25. 如图1,在四边形ABCD中,AC和BD相交于点O,$AO= CO$,$∠BCA= ∠CAD$.


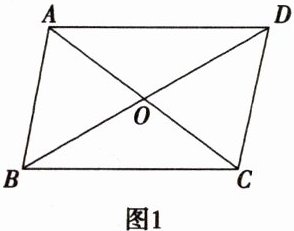
(1)求证：四边形ABCD是平行四边形；
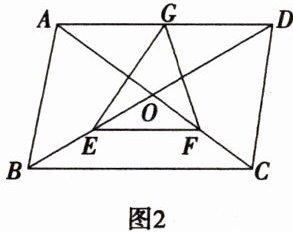
(2)如图2,E,F,G分别是BO,CO,AD的中点,连接EF,GE,GF,若$BD= 2AB$,$BC= 15$,$AC= 16$,求$\triangle EFG$的周长.

答案：
解:
(1) 证明: $ \because \angle B C A = \angle C A D $, $ \therefore A D // BC $, 在 $ \triangle A O D $ 与 $ \triangle C O B $ 中, $ \left\{ \begin{array} { l } { \angle B C A = \angle C A D } \\ { A O = C O } \\ { \angle A O D = \angle C O B } \end{array} \right. $, $ \therefore \triangle A O D \cong \triangle C O B ( \mathrm { ASA } ) $, $ \therefore A D = B C $, $ \therefore $ 四边形 $ A B C D $ 是平行四边形.
(2) 连接 $ D F $, 如图. $ \because $ 四边形 $ A B C D $ 是平行四边形, $ \therefore A D = B C = 15 $, $ A B = C D $, $ A D // B C $, $ B D = 2 O D $, $ O A = O C = \frac { 1 } { 2 } A C = 8 $, $ \because B D = 2 A B $, $ \therefore A B = O D $, $ \therefore D O = D C $, $ \because $ 点 $ F $ 是 $ O C $ 的中点, $ \therefore O F = \frac { 1 } { 2 } O C = 4 $, $ D F \perp O C $, $ \therefore A F = O A + O F = 12 $, 在 $ \mathrm { Rt } \triangle A F D $ 中, $ D F = \sqrt { A D ^ { 2 } - A F ^ { 2 } } = \sqrt { 15 ^ { 2 } - 12 ^ { 2 } } = 9 $, $ \therefore $ 点 $ G $ 是 $ A D $ 的中点, $ \angle A F D = 90 ^ { \circ } $, $ \therefore D G = F G = \frac { 1 } { 2 } A D = 7. 5 $, $ \because $ 点 $ E $, 点 $ F $ 分别是 $ O B $, $ O C $ 的中点, $ \therefore E F $ 是 $ \triangle O B C $ 的中位线, $ \therefore E F = \frac { 1 } { 2 } B C = 7. 5 $, $ E F // B C $, $ \therefore E F = D G $, $ E F // A D $, $ \therefore $ 四边形 $ G E F D $ 是平行四边形, $ \therefore G E = D F = 9 $, $ \therefore \triangle E F G $ 的周长 $ = G E + G F + E F = 9 + 7. 5 + 7. 5 = 24 $, $ \therefore \triangle E F G $ 的周长为 24.