2025年暑假作业内蒙古大学出版社八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业内蒙古大学出版社八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
5. 若$x = \sqrt{2} + 1$,则代数式$x^2 - 2x + 2$的值为(
A.7
B.4
C.3
D.$3 - 2\sqrt{2}$
C
)A.7
B.4
C.3
D.$3 - 2\sqrt{2}$
答案:
解:因为$x = \sqrt{2} + 1$,所以$x - 1 = \sqrt{2}$。
$x^2 - 2x + 2 = (x^2 - 2x + 1) + 1 = (x - 1)^2 + 1$
将$x - 1 = \sqrt{2}$代入上式,得$(\sqrt{2})^2 + 1 = 2 + 1 = 3$。
答案:C
$x^2 - 2x + 2 = (x^2 - 2x + 1) + 1 = (x - 1)^2 + 1$
将$x - 1 = \sqrt{2}$代入上式,得$(\sqrt{2})^2 + 1 = 2 + 1 = 3$。
答案:C
1. 使$\sqrt{x - 2}$有意义的x的取值范围在数轴上表示为(
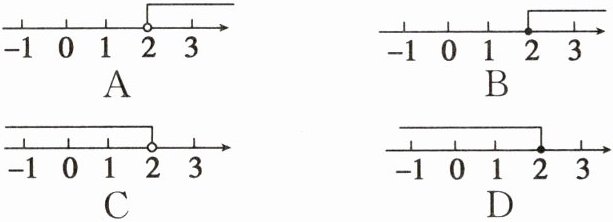
A.
B.
C.
D.
B
)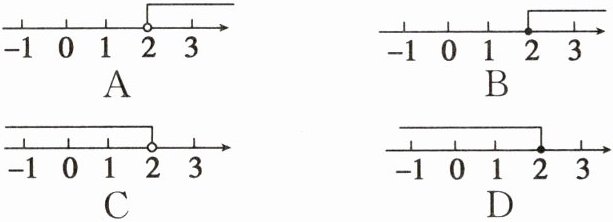
A.
B.
C.
D.
答案:
要使$\sqrt{x - 2}$有意义,则被开方数须为非负数,即$x - 2 \geq 0$,解得$x \geq 2$。在数轴上表示为从2出发向右的射线,2处为实心点,对应选项B。
B
B
2. 下列计算正确的是(
A.$\sqrt[3]{-8} = 2$
B.$\sqrt{(-3)^2} = -3$
C.$2\sqrt{5} + 3\sqrt{5} = 5\sqrt{5}$
D.$(\sqrt{2} + 1)^2 = 3$
C
)A.$\sqrt[3]{-8} = 2$
B.$\sqrt{(-3)^2} = -3$
C.$2\sqrt{5} + 3\sqrt{5} = 5\sqrt{5}$
D.$(\sqrt{2} + 1)^2 = 3$
答案:
解:A.$\sqrt[3]{-8}=-2$,故A错误;
B.$\sqrt{(-3)^2}=\sqrt{9}=3$,故B错误;
C.$2\sqrt{5}+3\sqrt{5}=5\sqrt{5}$,故C正确;
D.$(\sqrt{2}+1)^2=(\sqrt{2})^2+2×\sqrt{2}×1+1^2=2+2\sqrt{2}+1=3+2\sqrt{2}$,故D错误。
结论:C
B.$\sqrt{(-3)^2}=\sqrt{9}=3$,故B错误;
C.$2\sqrt{5}+3\sqrt{5}=5\sqrt{5}$,故C正确;
D.$(\sqrt{2}+1)^2=(\sqrt{2})^2+2×\sqrt{2}×1+1^2=2+2\sqrt{2}+1=3+2\sqrt{2}$,故D错误。
结论:C
3. 下列说法不正确的是(
A.$\sqrt{a}(a \geq 0)$是二次根式
B.当$a < 0$时,$(\sqrt{a})^2 = -a$
C.$\sqrt{a^2 + b}$是最简二次根式
D.$\sqrt{(x + 3)^2} = x + 3成立的条件是x \geq -3$
B
)A.$\sqrt{a}(a \geq 0)$是二次根式
B.当$a < 0$时,$(\sqrt{a})^2 = -a$
C.$\sqrt{a^2 + b}$是最简二次根式
D.$\sqrt{(x + 3)^2} = x + 3成立的条件是x \geq -3$
答案:
解:
A. √a(a≥0)是二次根式,正确。
B. 当a<0时,√a无意义,故原说法不正确。
C. √(a² + b)是最简二次根式,正确。
D. √(x + 3)² = x + 3成立的条件是x + 3≥0,即x≥-3,正确。
答案:B
A. √a(a≥0)是二次根式,正确。
B. 当a<0时,√a无意义,故原说法不正确。
C. √(a² + b)是最简二次根式,正确。
D. √(x + 3)² = x + 3成立的条件是x + 3≥0,即x≥-3,正确。
答案:B
4. 把$(a - b)\sqrt{-\frac{1}{a - b}}(a < b)$化成最简二次根式,正确的是(
A.$\sqrt{b - a}$
B.$\sqrt{a - b}$
C.$-\sqrt{b - a}$
D.$-\sqrt{a - b}$
C
)A.$\sqrt{b - a}$
B.$\sqrt{a - b}$
C.$-\sqrt{b - a}$
D.$-\sqrt{a - b}$
答案:
解:
∵$a < b$,
∴$a - b < 0$,则$-(a - b) = b - a > 0$。
$(a - b)\sqrt{-\frac{1}{a - b}} = (a - b)\sqrt{\frac{1}{b - a}} = (a - b)\frac{\sqrt{1}}{\sqrt{b - a}} = (a - b)\frac{1}{\sqrt{b - a}}$
分子分母同乘$\sqrt{b - a}$得:$(a - b)\frac{\sqrt{b - a}}{b - a} = -\sqrt{b - a}$
答案:C
∵$a < b$,
∴$a - b < 0$,则$-(a - b) = b - a > 0$。
$(a - b)\sqrt{-\frac{1}{a - b}} = (a - b)\sqrt{\frac{1}{b - a}} = (a - b)\frac{\sqrt{1}}{\sqrt{b - a}} = (a - b)\frac{1}{\sqrt{b - a}}$
分子分母同乘$\sqrt{b - a}$得:$(a - b)\frac{\sqrt{b - a}}{b - a} = -\sqrt{b - a}$
答案:C
5. 若$a = \sqrt{2}$,$b = \sqrt{7}$,则$\sqrt{\frac{14a^2}{b^2}} = $(
A.2
B.4
C.$\sqrt{7}$
D.$\sqrt{2}$
A
)A.2
B.4
C.$\sqrt{7}$
D.$\sqrt{2}$
答案:
解:已知$a = \sqrt{2}$,$b = \sqrt{7}$,则$a^2 = (\sqrt{2})^2 = 2$,$b^2 = (\sqrt{7})^2 = 7$。
$\begin{aligned}\sqrt{\frac{14a^2}{b^2}}&=\sqrt{\frac{14×2}{7}}\\&=\sqrt{\frac{28}{7}}\\&=\sqrt{4}\\&=2\end{aligned}$
答案:A
$\begin{aligned}\sqrt{\frac{14a^2}{b^2}}&=\sqrt{\frac{14×2}{7}}\\&=\sqrt{\frac{28}{7}}\\&=\sqrt{4}\\&=2\end{aligned}$
答案:A
6. 与$\sqrt{3^2 - 2^2 - 1^2}$结果相同的是(
A.$3 - 2 + 1$
B.$3 + 2 - 1$
C.$3 + 2 + 1$
D.$3 - 2 - 1$
A
)A.$3 - 2 + 1$
B.$3 + 2 - 1$
C.$3 + 2 + 1$
D.$3 - 2 - 1$
答案:
解:计算原式:$\sqrt{3^2 - 2^2 - 1^2} = \sqrt{9 - 4 - 1} = \sqrt{4} = 2$
选项A:$3 - 2 + 1 = 2$,与原式结果相同。
选项B:$3 + 2 - 1 = 4 \neq 2$
选项C:$3 + 2 + 1 = 6 \neq 2$
选项D:$3 - 2 - 1 = 0 \neq 2$
答案:A
选项A:$3 - 2 + 1 = 2$,与原式结果相同。
选项B:$3 + 2 - 1 = 4 \neq 2$
选项C:$3 + 2 + 1 = 6 \neq 2$
选项D:$3 - 2 - 1 = 0 \neq 2$
答案:A
7. 对于任意的正数$m$,$n$,定义运算※:$m※n = \begin{cases} \sqrt{m} - \sqrt{n}(m \geq n) \\ \sqrt{m} + \sqrt{n}(m < n) \end{cases} $,计算$(3※2) × (8※12)$的结果为(
A.$2 - 4\sqrt{6}$
B.2
C.$2\sqrt{5}$
D.20
B
)A.$2 - 4\sqrt{6}$
B.2
C.$2\sqrt{5}$
D.20
答案:
解:
∵3>2,
∴3※2=√3 - √2;
∵8<12,
∴8※12=√8 + √12=2√2 + 2√3;
则(3※2)×(8※12)=(√3 - √2)(2√2 + 2√3)
=√3×2√2 + √3×2√3 - √2×2√2 - √2×2√3
=2√6 + 2×3 - 2×2 - 2√6
=2√6 + 6 - 4 - 2√6
=2.
答案:B
∵3>2,
∴3※2=√3 - √2;
∵8<12,
∴8※12=√8 + √12=2√2 + 2√3;
则(3※2)×(8※12)=(√3 - √2)(2√2 + 2√3)
=√3×2√2 + √3×2√3 - √2×2√2 - √2×2√3
=2√6 + 2×3 - 2×2 - 2√6
=2√6 + 6 - 4 - 2√6
=2.
答案:B
8. 估计$(2\sqrt{5} + 5\sqrt{2}) × \sqrt{\frac{1}{5}}$的值应在(
A.4和5之间
B.5和6之间
C.6和7之间
D.7和8之间
B
)A.4和5之间
B.5和6之间
C.6和7之间
D.7和8之间
答案:
解:$(2\sqrt{5} + 5\sqrt{2}) × \sqrt{\frac{1}{5}}$
$=2\sqrt{5}×\sqrt{\frac{1}{5}} + 5\sqrt{2}×\sqrt{\frac{1}{5}}$
$=2\sqrt{5×\frac{1}{5}} + 5\sqrt{\frac{2}{5}}$
$=2×1 + 5×\frac{\sqrt{10}}{5}$
$=2 + \sqrt{10}$
因为$3^2 = 9$,$4^2 = 16$,所以$3 < \sqrt{10} < 4$,则$2 + 3 < 2 + \sqrt{10} < 2 + 4$,即$5 < 2 + \sqrt{10} < 6$。
答案:B
$=2\sqrt{5}×\sqrt{\frac{1}{5}} + 5\sqrt{2}×\sqrt{\frac{1}{5}}$
$=2\sqrt{5×\frac{1}{5}} + 5\sqrt{\frac{2}{5}}$
$=2×1 + 5×\frac{\sqrt{10}}{5}$
$=2 + \sqrt{10}$
因为$3^2 = 9$,$4^2 = 16$,所以$3 < \sqrt{10} < 4$,则$2 + 3 < 2 + \sqrt{10} < 2 + 4$,即$5 < 2 + \sqrt{10} < 6$。
答案:B
9. 实数$a$,$b$在数轴上的位置如图所示,化简$(\sqrt{a})^2 + \sqrt{b^2}$的结果是(

A.$-a + b$
B.$-a - b$
C.$a + b$
D.$a - b$
D
)
A.$-a + b$
B.$-a - b$
C.$a + b$
D.$a - b$
答案:
由数轴可知:$a>1$,$b<0$。
因为$a>0$,所以$(\sqrt{a})^2 = a$;
因为$b<0$,所以$\sqrt{b^2} = |b| = -b$。
则$(\sqrt{a})^2 + \sqrt{b^2} = a + (-b) = a - b$。
D
因为$a>0$,所以$(\sqrt{a})^2 = a$;
因为$b<0$,所以$\sqrt{b^2} = |b| = -b$。
则$(\sqrt{a})^2 + \sqrt{b^2} = a + (-b) = a - b$。
D
10. 观察式子:$\sqrt{4 × 9} = \sqrt{36} = 6$,$\sqrt{4} × \sqrt{9} = 2 × 3 = 6$;$\sqrt{\frac{49}{100} × \frac{9}{4}} = \sqrt{\frac{441}{400}} = \frac{21}{20}$,$\sqrt{\frac{49}{100}} × \sqrt{\frac{9}{4}} = \frac{7}{10} × \frac{3}{2} = \frac{21}{20}$;$\sqrt{0.25 × 0.04} = \sqrt{0.01} = 0.1$,$\sqrt{0.25} × \sqrt{0.04} = 0.5 × 0.2 = 0.1$。由此猜想$\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}(a \geq 0, b \geq 0)$。上述探究过程蕴含的思想方法是(
A.特殊与一般
B.类比
C.转化
D.公理化
A
)A.特殊与一般
B.类比
C.转化
D.公理化
答案:
通过观察多个特殊例子:$\sqrt{4×9}=\sqrt{4}×\sqrt{9}$,$\sqrt{\frac{49}{100}×\frac{9}{4}}=\sqrt{\frac{49}{100}}×\sqrt{\frac{9}{4}}$,$\sqrt{0.25×0.04}=\sqrt{0.25}×\sqrt{0.04}$,从这些具体的特殊情况归纳猜想出一般结论$\sqrt{ab}=\sqrt{a}·\sqrt{b}(a\geq0,b\geq0)$。此过程是从特殊到一般的推理。
A
A
查看更多完整答案,请扫码查看


