《2025年暑假作业内蒙古大学出版社八年级数学》

4. 小丽从甲地匀速步行去乙地,小华骑自行车从乙地匀速前往甲地,同时出发。两人离甲地的距离$y(m)与出发时间x(min)$之间的函数关系如图所示。

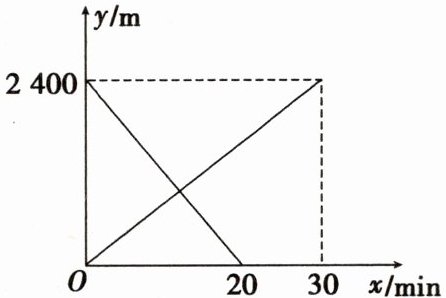
(1)小丽步行的速度为____80$m/min$；
(2)当两人相遇时,求他们到甲地的距离。
解：由图象可得，小华骑自行车的速度是 $\frac{2400}{20} = 120(m/min)$。
∴出发后需要 $\frac{2400}{120 + 80} = 12(min)$ 两人相遇。
∴相遇时小丽所走的路程为 $12×80 = 960(m)$，即当两人相遇时，他们到甲地的距离是 $960m$。

答案： 4. 解:
(1)由图象可知，小丽步行的速度为 $\frac{2400}{30} = 80(m/min)$。
(2)由图象可得，小华骑自行车的速度是 $\frac{2400}{20} = 120(m/min)$。
∴出发后需要 $\frac{2400}{120 + 80} = 12(min)$ 两人相遇。
∴相遇时小丽所走的路程为 $12×80 = 960(m)$，即当两人相遇时，他们到甲地的距离是 $960m$。

1. 水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为$C = 2\pi r。$下列判断正确的是(C)
A.2是变量
B.$\pi$是变量
C.$r$是变量
D.$C$是常量

答案： 在圆周长公式$C = 2\pi r$中，$2$和$\pi$是固定不变的常数，称为常量；$r$是可以变化的半径，$C$是随着$r$的变化而变化的周长，所以$r$和$C$是变量。
A. $2$是常量，不是变量，故A错误；
B. $\pi$是常量，不是变量，故B错误；
C. $r$是变量，故C正确；
D. $C$是变量，不是常量，故D错误。
答案：C

2. 函数$y = \frac{x}{\sqrt{x + 3}}+\frac{1}{x - 1}的自变量x$的取值范围是(B)
A.$x \neq -3且x \neq 1$
B.$x ＞ -3且x \neq 1$
C.$x ＞ -3$
D.$x \geq -3且x \neq 1$

答案： 要使函数$y = \frac{x}{\sqrt{x + 3}}+\frac{1}{x - 1}$有意义，需满足：
1. 对于$\frac{x}{\sqrt{x + 3}}$，根号下的数须大于0，即$x + 3 ＞ 0$，解得$x ＞ -3$；
2. 对于$\frac{1}{x - 1}$，分母不能为0，即$x - 1 \neq 0$，解得$x \neq 1$。
综上，自变量$x$的取值范围是$x ＞ -3$且$x \neq 1$。
答案：B

3. 将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度$h(cm)与注水时间t(min)$的函数图象大致为(B)

答案： 解：注水初期，大容器内水面低于小水杯杯口，小水杯中水面高度保持不变；当大容器内水面达到小水杯杯口后，继续注水，小水杯中水面高度随注水时间匀速上升。函数图象先水平后上升，大致为选项B。
答案：B

4. 若一次函数$y= (k + 3)x - 1的函数值y随x$的增大而减小,则$k$值可能是(D)
A.2
B.$\frac{3}{2}$
C.$-\frac{1}{2}$
D.$-4$

答案： 解：对于一次函数$y=(k + 3)x - 1$，当函数值$y$随$x$的增大而减小时，其斜率$k + 3\lt 0$，解得$k\lt - 3$。
选项中只有$-4\lt - 3$，所以$k$值可能是$-4$。
答案：D

5. 已知$(x_1,y_1)$,$(x_2,y_2)$,$(x_3,y_3)为直线y = -2x + 3$上的三个点,且$x_1 ＜ x_2 ＜ x_3$,则以下判断正确的是(D)
A.若$x_1x_2 ＞ 0$,则$y_1y_3 ＞ 0$
B.若$x_1x_3 ＜ 0$,则$y_1y_2 ＞ 0$
C.若$x_2x_3 ＞ 0$,则$y_1y_3 ＞ 0$
D.若$x_2x_3 ＜ 0$,则$y_1y_2 ＞ 0$

答案： 解：直线$y=-2x+3$中，$k=-2＜0$，$y$随$x$增大而减小。
A. 若$x_1x_2＞0$，则$x_1$、$x_2$同号。
当$x_1＜x_2＜0$时，$x_3＞x_2＞0$，$y_1=-2x_1+3＞3$，$y_3=-2x_3+3＜3$，但$x_3$可能使$y_3＜0$，此时$y_1y_3＜0$，A错误。
B. 若$x_1x_3＜0$，则$x_1＜0＜x_3$。
$x_2$可能在$0$左侧或右侧，当$x_1＜x_2＜0$时，$y_1＞y_2＞3$，$y_1y_2＞0$；当$0＜x_2＜x_3$时，$y_1＞3$，$y_2＜3$，若$y_2＜0$，则$y_1y_2＜0$，B错误。
C. 若$x_2x_3＞0$，则$x_2$、$x_3$同号。
当$0＜x_2＜x_3$时，$x_1＜0$，$y_1＞3$，$y_3＜3$，若$y_3＜0$，$y_1y_3＜0$，C错误。
D. 若$x_2x_3＜0$，则$x_2＜0＜x_3$，且$x_1＜x_2＜0$，$y_1＞y_2＞3$，$y_1y_2＞0$，D正确。
答案：D