2025年暑假作业内蒙古大学出版社八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业内蒙古大学出版社八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 已知直角三角形的三边$a$,$b$,$c满足c>a>b$,分别以$a$,$b$,$c$为边作三个正方形,把两个较小的正方形放置在最大的正方形内,如图,设三个正方形无重叠部分的面积为$S_{1}$,均重叠部分的面积为$S_{2}$,则 (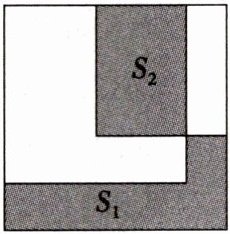
A.$S_{1}>S_{2}$
B.$S_{1}<S_{2}$
C.$S_{1}= S_{2}$
D.$S_{1}$,$S_{2}$的大小无法确定
C
)
A.$S_{1}>S_{2}$
B.$S_{1}<S_{2}$
C.$S_{1}= S_{2}$
D.$S_{1}$,$S_{2}$的大小无法确定
答案:
解:
∵直角三角形三边满足$c > a > b$,由勾股定理得$a^2 + b^2 = c^2$。
三个正方形面积分别为$a^2$、$b^2$、$c^2$。
最大正方形面积为$c^2$,两个小正方形面积和为$a^2 + b^2 = c^2$。
两个小正方形放置在最大正方形内,重叠部分面积为$S_2$,则覆盖总面积为$a^2 + b^2 - S_2 = c^2 - S_2$。
无重叠部分面积$S_1 = c^2 - (c^2 - S_2) = S_2$。
∴$S_1 = S_2$。
答案:C
∵直角三角形三边满足$c > a > b$,由勾股定理得$a^2 + b^2 = c^2$。
三个正方形面积分别为$a^2$、$b^2$、$c^2$。
最大正方形面积为$c^2$,两个小正方形面积和为$a^2 + b^2 = c^2$。
两个小正方形放置在最大正方形内,重叠部分面积为$S_2$,则覆盖总面积为$a^2 + b^2 - S_2 = c^2 - S_2$。
无重叠部分面积$S_1 = c^2 - (c^2 - S_2) = S_2$。
∴$S_1 = S_2$。
答案:C
2. 如图,“今有竹高两丈五尺,末折抵地,去本五尺,问折者高几何?”意思是:一根竹子,原来高两丈五尺(一丈为十尺),将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部五尺远,则折断处离地面的高度为 (
A.5尺
B.25尺
C.13尺
D.12尺
D
)A.5尺
B.25尺
C.13尺
D.12尺
答案:
解:设折断处离地面的高度为 $ x $ 尺,则折断部分的长度为 $ (25 - x) $ 尺。
根据勾股定理,得 $ x^2 + 5^2 = (25 - x)^2 $。
展开得 $ x^2 + 25 = 625 - 50x + x^2 $。
化简得 $ 50x = 600 $,解得 $ x = 12 $。
D
根据勾股定理,得 $ x^2 + 5^2 = (25 - x)^2 $。
展开得 $ x^2 + 25 = 625 - 50x + x^2 $。
化简得 $ 50x = 600 $,解得 $ x = 12 $。
D
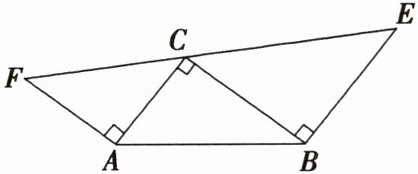
3. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AB= 6$,若以$AC边和BC边向外作等腰直角三角形AFC和等腰直角三角形BEC$。若$\triangle BEC的面积为S_{1}$,$\triangle AFC的面积为S_{2}$,则$S_{1}+S_{2}= $ (
A.4
B.9
C.18
D.36
C
)
A.4
B.9
C.18
D.36
答案:
解:在$Rt\triangle ABC$中,$\angle ACB=90^{\circ}$,$AB=6$,由勾股定理得$AC^{2}+BC^{2}=AB^{2}=6^{2}=36$。
因为$\triangle AFC$是等腰直角三角形,所以$AF=AC$,$\angle FAC=90^{\circ}$,则$S_{2}=\frac{1}{2}AC\cdot AF=\frac{1}{2}AC^{2}$。
因为$\triangle BEC$是等腰直角三角形,所以$BE=BC$,$\angle EBC=90^{\circ}$,则$S_{1}=\frac{1}{2}BC\cdot BE=\frac{1}{2}BC^{2}$。
所以$S_{1}+S_{2}=\frac{1}{2}BC^{2}+\frac{1}{2}AC^{2}=\frac{1}{2}(AC^{2}+BC^{2})=\frac{1}{2}×36=18$。
答案:C
因为$\triangle AFC$是等腰直角三角形,所以$AF=AC$,$\angle FAC=90^{\circ}$,则$S_{2}=\frac{1}{2}AC\cdot AF=\frac{1}{2}AC^{2}$。
因为$\triangle BEC$是等腰直角三角形,所以$BE=BC$,$\angle EBC=90^{\circ}$,则$S_{1}=\frac{1}{2}BC\cdot BE=\frac{1}{2}BC^{2}$。
所以$S_{1}+S_{2}=\frac{1}{2}BC^{2}+\frac{1}{2}AC^{2}=\frac{1}{2}(AC^{2}+BC^{2})=\frac{1}{2}×36=18$。
答案:C
4. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点。如图,在$6×6的正方形网格图形ABCD$中,$M$,$N分别是AB$,$BC$上的格点,$BM= 4$,$BN= 2$。若点$P$是这个网格图形中的格点,连接$PM$,$PN$,则所有满足$\angle MPN= 45^{\circ}的\triangle PMN$中,边$PM$的长的最大值是 (
A.$4\sqrt{2}$
B.6
C.$2\sqrt{10}$
D.$3\sqrt{5}$
C
)A.$4\sqrt{2}$
B.6
C.$2\sqrt{10}$
D.$3\sqrt{5}$
答案:
解:以点B为坐标原点,BC所在直线为x轴,BA所在直线为y轴建立平面直角坐标系。
则M(0,4),N(2,0)。
设P(x,y),x,y为整数,且0≤x≤6,0≤y≤6。
∵∠MPN=45°,
∴点P在以MN为弦的圆上,且圆心在MN的垂直平分线上,劣弧MN所对圆心角为90°。
MN中点坐标为(1,2),MN斜率为(0-4)/(2-0)=-2,
∴MN垂直平分线斜率为1/2,方程为y-2=(1/2)(x-1),即y=(1/2)x + 3/2。
设圆心为(2t-1, t+2),半径r,
则r²=(2t-1-0)²+(t+2-4)²=(2t-1)²+(t-2)²=5t²-8t+5,
且圆心到MN距离d=|(1/2)(2t-1)- (t+2)+ 3/2|/√[(1/2)²+1]=|t - 1/2 - t - 2 + 3/2|/√(5/4)=| -2 |/ (√5/2)=4√5/5,
∵d² + (MN/2)² = r²,MN=√(2²+4²)=2√5,(MN/2)=√5,
∴(16/5) + 5 = r²,即r²=41/5,
又r²=5t²-8t+5=41/5,解得t=4/5或t=0(舍),
则圆心为(2×4/5 -1, 4/5 + 2)=(3/5,14/5),
圆方程为(x - 3/5)² + (y - 14/5)²=41/5。
也可考虑优弧MN所对圆心角为270°的情况,同理可得另一圆方程。
经检验格点P可能坐标:
P(6,6)时,PM=√[(6-0)²+(6-4)²]=√(36+4)=√40=2√10;
P(4,6)时,PM=√(16+4)=√20=2√5;
P(6,2)时,PM=√(36+4)=√40=2√10;
P(0,0)时,PM=4;
P(2,6)时,PM=√(4+4)=2√2;
P(6,0)时,PM=√(36+16)=√52=2√13;
P(0,2)时,PM=√(0+4)=2;
P(4,0)时,PM=√(16+16)=4√2;
P(2,2)时,PM=√(4+4)=2√2;
P(5,5)时,PM=√(25+1)=√26;
P(5,3)时,PM=√(25+1)=√26;
P(3,5)时,PM=√(9+1)=√10;
P(3,3)时,PM=√(9+1)=√10;
P(1,5)时,PM=√(1+1)=√2;
P(1,3)时,PM=√(1+1)=√2;
P(0,6)时,PM=√(0+4)=2;
P(6,4)时,PM=√(36+0)=6;
P(4,4)时,PM=√(16+0)=4;
P(2,4)时,PM=√(4+0)=2;
P(0,2)时,PM=2;
P(6,2)时,2√10;
P(6,6)时,2√10;
比较所有PM长度:2√10≈6.32,6,4√2≈5.66,2√13≈7.21(舍,经检验P(6,0)不满足∠MPN=45°),
∴PM最大值为2√10。
答案:C
则M(0,4),N(2,0)。
设P(x,y),x,y为整数,且0≤x≤6,0≤y≤6。
∵∠MPN=45°,
∴点P在以MN为弦的圆上,且圆心在MN的垂直平分线上,劣弧MN所对圆心角为90°。
MN中点坐标为(1,2),MN斜率为(0-4)/(2-0)=-2,
∴MN垂直平分线斜率为1/2,方程为y-2=(1/2)(x-1),即y=(1/2)x + 3/2。
设圆心为(2t-1, t+2),半径r,
则r²=(2t-1-0)²+(t+2-4)²=(2t-1)²+(t-2)²=5t²-8t+5,
且圆心到MN距离d=|(1/2)(2t-1)- (t+2)+ 3/2|/√[(1/2)²+1]=|t - 1/2 - t - 2 + 3/2|/√(5/4)=| -2 |/ (√5/2)=4√5/5,
∵d² + (MN/2)² = r²,MN=√(2²+4²)=2√5,(MN/2)=√5,
∴(16/5) + 5 = r²,即r²=41/5,
又r²=5t²-8t+5=41/5,解得t=4/5或t=0(舍),
则圆心为(2×4/5 -1, 4/5 + 2)=(3/5,14/5),
圆方程为(x - 3/5)² + (y - 14/5)²=41/5。
也可考虑优弧MN所对圆心角为270°的情况,同理可得另一圆方程。
经检验格点P可能坐标:
P(6,6)时,PM=√[(6-0)²+(6-4)²]=√(36+4)=√40=2√10;
P(4,6)时,PM=√(16+4)=√20=2√5;
P(6,2)时,PM=√(36+4)=√40=2√10;
P(0,0)时,PM=4;
P(2,6)时,PM=√(4+4)=2√2;
P(6,0)时,PM=√(36+16)=√52=2√13;
P(0,2)时,PM=√(0+4)=2;
P(4,0)时,PM=√(16+16)=4√2;
P(2,2)时,PM=√(4+4)=2√2;
P(5,5)时,PM=√(25+1)=√26;
P(5,3)时,PM=√(25+1)=√26;
P(3,5)时,PM=√(9+1)=√10;
P(3,3)时,PM=√(9+1)=√10;
P(1,5)时,PM=√(1+1)=√2;
P(1,3)时,PM=√(1+1)=√2;
P(0,6)时,PM=√(0+4)=2;
P(6,4)时,PM=√(36+0)=6;
P(4,4)时,PM=√(16+0)=4;
P(2,4)时,PM=√(4+0)=2;
P(0,2)时,PM=2;
P(6,2)时,2√10;
P(6,6)时,2√10;
比较所有PM长度:2√10≈6.32,6,4√2≈5.66,2√13≈7.21(舍,经检验P(6,0)不满足∠MPN=45°),
∴PM最大值为2√10。
答案:C
5. $\triangle ABC的三边长a$,$b$,$c满足(a-b)^{2}+\sqrt{2a-b-3}+|c-3\sqrt{2}|= 0$,则$\triangle ABC$是
等腰直角三角形
。
答案:
解:因为$(a - b)^2 + \sqrt{2a - b - 3} + |c - 3\sqrt{2}| = 0$,且$(a - b)^2 \geq 0$,$\sqrt{2a - b - 3} \geq 0$,$|c - 3\sqrt{2}| \geq 0$,所以可得:
$\begin{cases}a - b = 0 \\ 2a - b - 3 = 0 \\ c - 3\sqrt{2} = 0\end{cases}$
由$a - b = 0$得$a = b$,将$a = b$代入$2a - b - 3 = 0$,得$2a - a - 3 = 0$,解得$a = 3$,所以$b = 3$,由$c - 3\sqrt{2} = 0$得$c = 3\sqrt{2}$。
因为$a^2 + b^2 = 3^2 + 3^2 = 18$,$c^2 = (3\sqrt{2})^2 = 18$,所以$a^2 + b^2 = c^2$,且$a = b$,故$\triangle ABC$是等腰直角三角形。
等腰直角三角形
$\begin{cases}a - b = 0 \\ 2a - b - 3 = 0 \\ c - 3\sqrt{2} = 0\end{cases}$
由$a - b = 0$得$a = b$,将$a = b$代入$2a - b - 3 = 0$,得$2a - a - 3 = 0$,解得$a = 3$,所以$b = 3$,由$c - 3\sqrt{2} = 0$得$c = 3\sqrt{2}$。
因为$a^2 + b^2 = 3^2 + 3^2 = 18$,$c^2 = (3\sqrt{2})^2 = 18$,所以$a^2 + b^2 = c^2$,且$a = b$,故$\triangle ABC$是等腰直角三角形。
等腰直角三角形
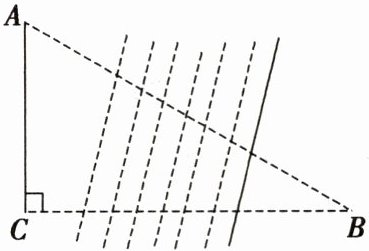
6. 如图,某数学兴趣小组为测量学校$C与河对岸工厂B$之间的距离,在学校附近选一点$A$,利用测量仪器测得$\angle A= 60^{\circ}$,$\angle C= 90^{\circ}$,$AC= 1km$。据此,可求得学校与工厂之间的距离$BC$等于
√3
$km$。
答案:
解:在Rt△ABC中,∠C=90°,∠A=60°,AC=1km,
tan∠A=BC/AC,
tan60°=BC/1,
BC=tan60°×1=√3×1=√3km。
故答案为√3。
tan∠A=BC/AC,
tan60°=BC/1,
BC=tan60°×1=√3×1=√3km。
故答案为√3。
7. 在一次“探究性学习”中,老师设计了如下数表:
| $n$ | 2 | 3 | 4 | 5 | 6 | …$$ |
| $a$ | $2^{2}-1$ | $3^{2}-1$ | $4^{2}-1$ | $5^{2}-1$ | $6^{2}-1$ | …$$ |
| $b$ | 4 | 6 | 8 | 10 | 12 | …$$ |
| $c$ | $2^{2}+1$ | $3^{2}+1$ | $4^{2}+1$ | $5^{2}+1$ | $6^{2}+1$ | …$$ |
(1)观察上表,用含$n$($n>1且n$为整数)的代数式表示$a$,$b$,$c$,则$a=$
(2)在(1)的条件下判断:以$a$,$b$,$c$为三边长的三角形是否为直角三角形?请说明理由。
(2) 以$a$,$b$,$c$为三边长的三角形是直角三角形,理由如下:
$\because a=n^{2}-1$,$b=2n$,$c=n^{2}+1$
$\therefore a^{2}=(n^{2}-1)^{2}=n^{4}-2n^{2}+1$,$b^{2}=(2n)^{2}=4n^{2}$,$c^{2}=(n^{2}+1)^{2}=n^{4}+2n^{2}+1$
$\because a^{2}+b^{2}=n^{4}-2n^{2}+1 + 4n^{2}=n^{4}+2n^{2}+1$
$\therefore a^{2}+b^{2}=c^{2}$
$\therefore$ 以$a$,$b$,$c$为三边长的三角形是直角三角形
| $n$ | 2 | 3 | 4 | 5 | 6 | …$$ |
| $a$ | $2^{2}-1$ | $3^{2}-1$ | $4^{2}-1$ | $5^{2}-1$ | $6^{2}-1$ | …$$ |
| $b$ | 4 | 6 | 8 | 10 | 12 | …$$ |
| $c$ | $2^{2}+1$ | $3^{2}+1$ | $4^{2}+1$ | $5^{2}+1$ | $6^{2}+1$ | …$$ |
(1)观察上表,用含$n$($n>1且n$为整数)的代数式表示$a$,$b$,$c$,则$a=$
$n^{2}-1$
,$b=$$2n$
,$c=$$n^{2}+1$
。(2)在(1)的条件下判断:以$a$,$b$,$c$为三边长的三角形是否为直角三角形?请说明理由。
(2) 以$a$,$b$,$c$为三边长的三角形是直角三角形,理由如下:
$\because a=n^{2}-1$,$b=2n$,$c=n^{2}+1$
$\therefore a^{2}=(n^{2}-1)^{2}=n^{4}-2n^{2}+1$,$b^{2}=(2n)^{2}=4n^{2}$,$c^{2}=(n^{2}+1)^{2}=n^{4}+2n^{2}+1$
$\because a^{2}+b^{2}=n^{4}-2n^{2}+1 + 4n^{2}=n^{4}+2n^{2}+1$
$\therefore a^{2}+b^{2}=c^{2}$
$\therefore$ 以$a$,$b$,$c$为三边长的三角形是直角三角形
答案:
(1) $n^{2}-1$,$2n$,$n^{2}+1$
(2) 以$a$,$b$,$c$为三边长的三角形是直角三角形,理由如下:
$\because a=n^{2}-1$,$b=2n$,$c=n^{2}+1$
$\therefore a^{2}=(n^{2}-1)^{2}=n^{4}-2n^{2}+1$,$b^{2}=(2n)^{2}=4n^{2}$,$c^{2}=(n^{2}+1)^{2}=n^{4}+2n^{2}+1$
$\because a^{2}+b^{2}=n^{4}-2n^{2}+1 + 4n^{2}=n^{4}+2n^{2}+1$
$\therefore a^{2}+b^{2}=c^{2}$
$\therefore$ 以$a$,$b$,$c$为三边长的三角形是直角三角形
(1) $n^{2}-1$,$2n$,$n^{2}+1$
(2) 以$a$,$b$,$c$为三边长的三角形是直角三角形,理由如下:
$\because a=n^{2}-1$,$b=2n$,$c=n^{2}+1$
$\therefore a^{2}=(n^{2}-1)^{2}=n^{4}-2n^{2}+1$,$b^{2}=(2n)^{2}=4n^{2}$,$c^{2}=(n^{2}+1)^{2}=n^{4}+2n^{2}+1$
$\because a^{2}+b^{2}=n^{4}-2n^{2}+1 + 4n^{2}=n^{4}+2n^{2}+1$
$\therefore a^{2}+b^{2}=c^{2}$
$\therefore$ 以$a$,$b$,$c$为三边长的三角形是直角三角形
查看更多完整答案,请扫码查看


