《2025年暑假作业内蒙古大学出版社八年级数学》

1. 已知$n＞0$,若$\sqrt {2n}$是最简二次根式,请写出一个符合条件的$n$的正整数值1.

答案： 1(答案不唯一)

2. 如图,在四边形$ABCD$中,$AB// DC$,$AD// BC$,在不添加任何辅助线的前提下,要想四边形$ABCD$成为一个矩形,只需添加的一个条件是∠A = 90°(答案不唯一).

答案： ∠A = 90°(答案不唯一)

3. 已知直线$y_{1}= x-1与y_{2}= kx+b相交于点(2,1)$. 请写出一个$b$值0(写出一个即可),使$x＞2$时,$y_{1}＞y_{2}$.

答案： 解：因为直线$y_{1}=x - 1$与$y_{2}=kx + b$相交于点$(2,1)$，所以将$(2,1)$代入$y_{2}=kx + b$，得$1 = 2k + b$，即$b=1 - 2k$。
当$x＞2$时，$y_{1}＞y_{2}$，即$x - 1＞kx + b$。将$b=1 - 2k$代入，得$x - 1＞kx + 1 - 2k$，移项化简得$(1 - k)x＞2 - 2k$，即$(1 - k)(x - 2)＞0$。
因为$x＞2$，所以$x - 2＞0$，则$1 - k＞0$，即$k＜1$。
取$k = 0$，则$b=1 - 2×0=1$；取$k = 0.5$，则$b=1 - 2×0.5=0$等，所以$b$可以为$0$。
0

4. 请写出一个函数的表达式,使得它的图象经过点$(2,0)$：y = x - 2(答案不唯一).

答案： y = x - 2(答案不唯一)

5. 如图,点$E$,$F分别在□ ABCD的边AB$,$BC$上,$AE= CF$,连接$DE$,$DF$. 请从以下三个条件：①$∠1= ∠2$；②$DE= DF$；③$∠3= ∠4$中,选择一个合适的作为已知条件,使$□ ABCD$为菱形.

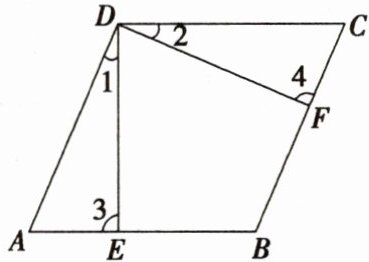
(1)你添加的条件是①或③(填序号)；
(2)添加了条件后,请证明$□ ABCD$为菱形.
证明：
情况一：添加条件①
∵四边形ABCD是平行四边形
∴∠A=∠C
在△ADE和△CDF中
$\left\{\begin{array}{l} ∠1=∠2\\ ∠A=∠C\\ AE=CF\end{array}\right.$
∴△ADE≌△CDF(AAS)
∴AD=CD
∴□ABCD为菱形
情况二：添加条件③
∵四边形ABCD是平行四边形
∴∠A=∠C
在△ADE和△CDF中
$\left\{\begin{array}{l} ∠3=∠4\\ AE=CF\\ ∠A=∠C\end{array}\right.$
∴△ADE≌△CDF(ASA)
∴AD=CD
∴□ABCD为菱形

答案：
(1)①或③
(2)证明：
情况一：添加条件①
∵四边形ABCD是平行四边形
∴∠A=∠C
在△ADE和△CDF中
$\left\{\begin{array}{l} ∠1=∠2\\ ∠A=∠C\\ AE=CF\end{array}\right.$
∴△ADE≌△CDF(AAS)
∴AD=CD
∴□ABCD为菱形
情况二：添加条件③
∵四边形ABCD是平行四边形
∴∠A=∠C
在△ADE和△CDF中
$\left\{\begin{array}{l} ∠3=∠4\\ AE=CF\\ ∠A=∠C\end{array}\right.$
∴△ADE≌△CDF(ASA)
∴AD=CD
∴□ABCD为菱形

1. 某村对产出的稻虾米进行线上销售,连续7天的销量分别为:105,103,105,110,108,105,108(单位:袋),这组数据的众数和中位数分别是 (B)
A.105,108
B.105,105
C.108,105
D.108,108

答案： 解：将数据从小到大排列：103,105,105,105,108,108,110
众数是出现次数最多的数，105出现3次，故众数为105；
中位数是第4个数，为105。
答案：B

2. 学校举行物理科技创新比赛,各项成绩均按百分制计,然后按照理论知识占20%,创新设计占50%,现场展示占30%计算选手的综合成绩(百分制).某同学本次比赛的各项成绩分别是:理论知识85分,创新设计88分,现场展示90分,那么该同学的综合成绩是88分.

答案： 解：综合成绩 = 85×20% + 88×50% + 90×30%
= 85×0.2 + 88×0.5 + 90×0.3
= 17 + 44 + 27
= 88
88