《2025年暑假作业内蒙古大学出版社八年级数学》

1. 如图,在正方形ABMF中剪去一个小正方形CDEM,动点P从点A出发,沿$A→B→C→D→E→F$的路线匀速运动到点F停止,则$\triangle APF$的面积S随着时间t的变化的图象大致是 (C)

答案： 解：设正方形ABMF边长为a，小正方形CDEM边长为b，点P运动速度为v。
1. 当P在AB上运动（0≤t≤a/v）：
AP=vt，△APF面积S=1/2·AP·AF=1/2·vt·a，S随t增大线性增大。
2. 当P在BC上运动（a/v＜t≤(a+b)/v）：
P到AF距离为a，△APF面积S=1/2·AF·a=1/2·a²，S为常数。
3. 当P在CD上运动（(a+b)/v＜t≤(a+2b)/v）：
P到AF距离为a-(vt-a)=2a+b-vt，S=1/2·a·(2a+b-vt)，S随t增大线性减小。
4. 当P在DE上运动（(a+2b)/v＜t≤(a+3b)/v）：
P到AF距离为a-b，S=1/2·a·(a-b)，S为常数。
5. 当P在EF上运动（(a+3b)/v＜t≤(a+4b)/v）：
PF=a+b-(vt-(a+3b))=2a+4b-vt，S=1/2·AF·PF=1/2·a·(2a+4b-vt)，S随t增大线性减小至0。
综上，面积变化趋势为：增大→不变→减小→不变→减小，图象大致是C。
答案：C

2. 如图,在等腰直角三角形ABC中,$∠BAC= 90^{\circ }$,点M,N分别为BC,AC上的动点,且$AN= CM,AB= \sqrt {2}$.当$AM+BN$的值最小时,CM的长为____$2-\sqrt{2}$.

答案： 解：以A为原点，AB,AC所在直线为x轴,y轴建立直角坐标系.
∵△ABC为等腰直角三角形,∠BAC=90°,AB=√2,
∴A(0,0),B(√2,0),C(0,√2),BC:y=-x+√2.
设CM=t,则AN=CM=t.
∵N在AC上,AC=√2,
∴N(0,t)(0≤t≤√2).
∵M在BC上,CM=t,BC=2,
∴BM=2-t.
设M(x,y),由BM=2-t及B(√2,0),得
x=√2 - (2-t)·cos45°=√2 - (2-t)·√2/2 = t√2/2,
y=0 + (2-t)·sin45°=(2-t)·√2/2,
即M(t√2/2,(2-t)√2/2).
AM=√[(t√2/2)² + ((2-t)√2/2)²]=√(t² - 2t + 2),
BN=√[(√2 - 0)² + (0 - t)²]=√(t² + 2).
设f(t)=AM+BN=√(t² - 2t + 2)+√(t² + 2),
求导得f’(t)=(t - 1)/√(t² - 2t + 2) + t/√(t² + 2).
令f’(t)=0,解得t=2 - √2.
当t=2 - √2时,f(t)最小,即AM+BN最小.
答案：$2-\sqrt{2}$

3. 如图,直线$y= 2x+4$与x轴交于点A,与y轴交于点B,点D为OB的中点,$□ OCDE$的顶点C在x轴上,顶点E在直线AB上,则$□ OCDE$的面积为____2.

答案： 解：
对于直线$y = 2x + 4$，
- 令$y = 0$，得$2x + 4 = 0$，解得$x = -2$，则$A(-2, 0)$；
- 令$x = 0$，得$y = 4$，则$B(0, 4)$。
点$D$为$OB$中点，$OB = 4$，故$D(0, 2)$。
设$C(c, 0)$（$c ＞ 0$），因$□OCDE$中$OC// DE$且$OC = DE$，$OC$在$x$轴上，$D(0, 2)$，则$E$点坐标为$(-c, 2)$（$DE$长度为$c$，方向与$OC$相反）。
点$E(-c, 2)$在直线$y = 2x + 4$上，代入得：
$2 = 2(-c) + 4$，
解得$c = 1$。
$□OCDE$的底$OC = 1$，高为$D$点纵坐标$2$，面积为$1×2 = 2$。
答案：$2$

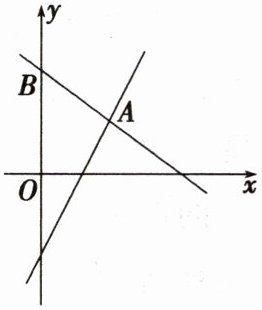
4. 如图,在直角坐标系中,点$A(2,m)在直线y= 2x-\frac {5}{2}$上,过点A的直线交y轴于点$B(0,3).$
(1)求m的值和直线AB的函数表达式;
(2)若点$P(t,y_{1})$在线段AB上,点$Q(t-1,y_{2})在直线y= 2x-\frac {5}{2}$上,求$y_{1}-y_{2}$的最大值.

答案： 解:
(1) 把 $A(2,m)$ 代入 $y = 2x-\frac{5}{2}$，解得 $m=\frac{3}{2}$。
设直线 $AB$ 的函数表达式为 $y = kx + b(k\neq0)$，把 $A(2,\frac{3}{2})$，$B(0,3)$ 代入得 $\begin{cases}2k + b=\frac{3}{2},\\b = 3,\end{cases}$ 解得 $\begin{cases}k=-\frac{3}{4},\\b = 3.\end{cases}$ $\therefore$ 直线 $AB$ 的函数表达式为 $y = -\frac{3}{4}x + 3$。
![img alt=4-2]
(2) $\because$ 点 $P(t,y_1)$ 在线段 $AB$ 上，点 $Q(t - 1,y_2)$ 在直线 $y = 2x-\frac{5}{2}$ 上，$\therefore y_1 = -\frac{3}{4}t + 3(0\leq t\leq2)$，$y_2 = 2(t - 1)-\frac{5}{2}=2t-\frac{9}{2}$，$\therefore y_1 - y_2 = -\frac{3}{4}t + 3-(2t-\frac{9}{2})=-\frac{11}{4}t+\frac{15}{2}(0\leq t\leq2)$。$\because -\frac{11}{4}＜0$，$\therefore y_1 - y_2$ 的值随 $t$ 的增大而减小，$\therefore$ 当 $t = 0$ 时，$y_1 - y_2$ 取得最大值，为 $\frac{15}{2}$。