2025年暑假作业内蒙古大学出版社八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业内蒙古大学出版社八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
例1 如图,在$□ ABCD$中,已知$AB = 12$,$AD = 8$,$\angle ABC的平分线BM交CD边于点M$,则$DM$的长为(
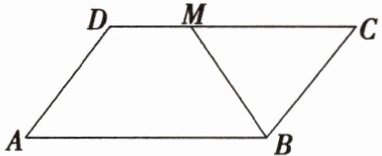
A.$2$
B.$4$
C.$6$
D.$8$
【答案】 B
方法总结:本题考查了平行四边形的性质、等腰三角形的判定以及平行线的性质等知识,熟练掌握平行四边形的性质,证明$MC = BC$是解题的关键。
B
)
A.$2$
B.$4$
C.$6$
D.$8$
【答案】 B
方法总结:本题考查了平行四边形的性质、等腰三角形的判定以及平行线的性质等知识,熟练掌握平行四边形的性质,证明$MC = BC$是解题的关键。
答案:
【解析】:本题可根据平行四边形的性质以及角平分线的性质,证明出$\triangle BCM$是等腰三角形,进而求出$DM$的长。
步骤一:根据平行四边形的性质得到相关线段和角的关系
已知四边形$ABCD$是平行四边形,根据平行四边形的性质:平行四边形的对边平行且相等,可得$AB// CD$,$AB = CD = 12$,$AD = BC = 8$。
因为$AB// CD$,根据两直线平行,内错角相等,所以$\angle ABM = \angle BMC$。
步骤二:根据角平分线的性质得到角的关系
因为$BM$是$\angle ABC$的平分线,所以$\angle ABM = \angle MBC$。
步骤三:通过等量代换证明$\triangle BCM$是等腰三角形
由$\angle ABM = \angle BMC$,$\angle ABM = \angle MBC$,通过等量代换可得$\angle MBC = \angle BMC$。
在$\triangle BCM$中,等角对等边,所以$MC = BC$。
已知$BC = 8$,则$MC = 8$。
步骤四:求出$DM$的长
因为$CD = 12$,$MC = 8$,所以$DM = CD - MC = 12 - 8 = 4$。
【答案】:B
步骤一:根据平行四边形的性质得到相关线段和角的关系
已知四边形$ABCD$是平行四边形,根据平行四边形的性质:平行四边形的对边平行且相等,可得$AB// CD$,$AB = CD = 12$,$AD = BC = 8$。
因为$AB// CD$,根据两直线平行,内错角相等,所以$\angle ABM = \angle BMC$。
步骤二:根据角平分线的性质得到角的关系
因为$BM$是$\angle ABC$的平分线,所以$\angle ABM = \angle MBC$。
步骤三:通过等量代换证明$\triangle BCM$是等腰三角形
由$\angle ABM = \angle BMC$,$\angle ABM = \angle MBC$,通过等量代换可得$\angle MBC = \angle BMC$。
在$\triangle BCM$中,等角对等边,所以$MC = BC$。
已知$BC = 8$,则$MC = 8$。
步骤四:求出$DM$的长
因为$CD = 12$,$MC = 8$,所以$DM = CD - MC = 12 - 8 = 4$。
【答案】:B
1. 如图,在$□ ABCD$中,$AB = 8$,点$E是AB$ 上一点,$AE = 3$,连接$DE$,过点$C作CF// DE$,交$AB的延长线于点F$,则$BF$的长为(
上一点,$AE = 3$,连接$DE$,过点$C作CF// DE$,交$AB的延长线于点F$,则$BF$的长为(
A.$5$
B.$4$
C.$3$
D.$2$
 上一点,$AE = 3$,连接$DE$,过点$C作CF// DE$,交$AB的延长线于点F$,则$BF$的长为(
上一点,$AE = 3$,连接$DE$,过点$C作CF// DE$,交$AB的延长线于点F$,则$BF$的长为(C
)A.$5$
B.$4$
C.$3$
D.$2$
答案:
解:
∵四边形ABCD是平行四边形,
∴AB=CD=8,AB//CD。
∵CF//DE,
∴四边形DEFC是平行四边形,
∴EF=CD=8。
∵AE=3,AB=8,
∴BE=AB-AE=8-3=5,
∴BF=EF-BE=8-5=3。
答案:C
∵四边形ABCD是平行四边形,
∴AB=CD=8,AB//CD。
∵CF//DE,
∴四边形DEFC是平行四边形,
∴EF=CD=8。
∵AE=3,AB=8,
∴BE=AB-AE=8-3=5,
∴BF=EF-BE=8-5=3。
答案:C
例2 如图,菱形$ABCD的对角线AC$,$BD相交于点O$,过点$D作DH\perp AB于点H$,连接$OH$,$OH = 4$,若菱形$ABCD的面积为32\sqrt{3}$,则$CD$的长为(
A.$4$
B.$4\sqrt{3}$
C.$8$
D.$8\sqrt{3}$
【答案】 C
方法总结:特殊平行四边形的性质与判定的综合应用是对学生综合能力的考查,解决此类问题的关键是熟练掌握特殊平行四边形的性质与判定,弄清题目条件,正确地选择性质或判定解决问题。
C
)A.$4$
B.$4\sqrt{3}$
C.$8$
D.$8\sqrt{3}$
【答案】 C
方法总结:特殊平行四边形的性质与判定的综合应用是对学生综合能力的考查,解决此类问题的关键是熟练掌握特殊平行四边形的性质与判定,弄清题目条件,正确地选择性质或判定解决问题。
答案:
解:
∵四边形ABCD是菱形,
∴AC⊥BD,AO=OC,BO=OD,AB=CD。
∵DH⊥AB,
∴∠DHB=90°,
∴OH是Rt△DHB斜边BD上的中线,
∴OH=1/2BD。
∵OH=4,
∴BD=8。
∵菱形ABCD的面积=1/2×AC×BD=32√3,
∴1/2×AC×8=32√3,解得AC=8√3,
∴AO=1/2AC=4√3,BO=1/2BD=4。
在Rt△AOB中,AB=√(AO²+BO²)=√[(4√3)²+4²]=√(48+16)=√64=8,
∴CD=AB=8。
答案:C
∵四边形ABCD是菱形,
∴AC⊥BD,AO=OC,BO=OD,AB=CD。
∵DH⊥AB,
∴∠DHB=90°,
∴OH是Rt△DHB斜边BD上的中线,
∴OH=1/2BD。
∵OH=4,
∴BD=8。
∵菱形ABCD的面积=1/2×AC×BD=32√3,
∴1/2×AC×8=32√3,解得AC=8√3,
∴AO=1/2AC=4√3,BO=1/2BD=4。
在Rt△AOB中,AB=√(AO²+BO²)=√[(4√3)²+4²]=√(48+16)=√64=8,
∴CD=AB=8。
答案:C
2. 如图,$E$,$F是正方形ABCD的对角线BD$上的两点,且$BE = DF$。
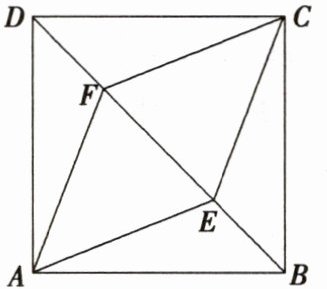
(1) 求证:$\triangle ABE\cong\triangle CDF$;
(2) 若$AB = 3\sqrt{2}$,$BE = 2$,求四边形$AECF$的面积。

(1) 求证:$\triangle ABE\cong\triangle CDF$;
(2) 若$AB = 3\sqrt{2}$,$BE = 2$,求四边形$AECF$的面积。
答案:
解:
(1) 证明:
∵四边形 ABCD 为正方形,
∴CD=AB,∠ABE=∠CDF=45°,
又
∵BE=DF,
∴△ABE≌△CDF(SAS).
(2) 连接 AC, 交 BD 于点 O,
∵四边形 ABCD 是正方形,
∴AC⊥BD,AO=CO,DO=BO,
又
∵DF=BE,
∴OE=OF,AO=CO,
∴四边形 AECF 是平行四边形,
∵AC⊥EF,
∴四边形 AECF 是菱形,
∵AB=3√2,
∴AC=BD=6,
∵BE=DF=2,
∴四边形 AECF 的面积=1/2AC·EF=1/2×6×2=6.

解:
(1) 证明:
∵四边形 ABCD 为正方形,
∴CD=AB,∠ABE=∠CDF=45°,
又
∵BE=DF,
∴△ABE≌△CDF(SAS).
(2) 连接 AC, 交 BD 于点 O,
∵四边形 ABCD 是正方形,
∴AC⊥BD,AO=CO,DO=BO,
又
∵DF=BE,
∴OE=OF,AO=CO,
∴四边形 AECF 是平行四边形,
∵AC⊥EF,
∴四边形 AECF 是菱形,
∵AB=3√2,
∴AC=BD=6,
∵BE=DF=2,
∴四边形 AECF 的面积=1/2AC·EF=1/2×6×2=6.

查看更多完整答案,请扫码查看


