《2025年假期园地暑假作业七年级数学人教版》

1. 不等式$-2x＜4$的解集是( )

A.$x＞-2$
B.$x＜-2$
C.$x＞2$
D.$x＜2$

答案： A

2. 把不等式$-2x＜4$的解集表示在数轴上,正确的是( )

答案： A

3. 不等式组$\left\{\begin{array}{l} 2x-1＜3,\\ x≥-1\end{array} \right. $的解集是( )

A.$x＜2$
B.$x≥-1$
C.$-1≤x＜2$
D.无解

答案： C

4. 把不等式组$\left\{\begin{array}{l} 2x+1＞-1,\\ x+2≤3\end{array} \right. $的解集表示在数轴上,下列选项正确的是( )

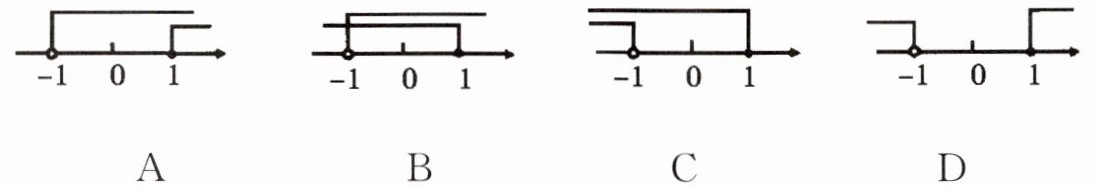
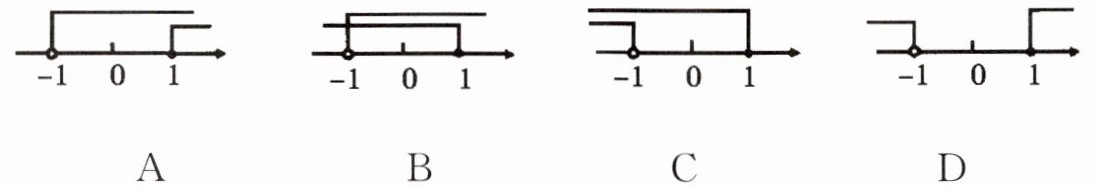
答案： B

5. 一个一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是( )


A.$-1≤x≤3$
B.$-1＜x≤3$
C.$x≥-1$
D.$x＜3$

答案： A

6. 若$\frac {1}{2}x^{2m-1}-8＞5$是一元一次不等式,则$m= $ _ .

答案： 1

7. 若$a= 2,b= 1与a= 3,b= 3都是方程b= ka+c$的解,则$k= $ _ ,$c= $ _ .

答案： 2 -3

8. 若$x＜-1$,则$x$ _ $\frac {1}{x}$(填“＞”“＜”或“=”).

答案： ＜

9. 在平面直角坐标系中,若点$P(x-2,x)$在第二象限,则$x$的取值范围是 _ .

答案： 0＜x＜2

10. 方程$2y+x= 7$的正整数解是 _ .

答案： 【解析】：
本题是一个二元一次方程求正整数解的问题。
需要找到满足方程$2y + x = 7$的所有正整数解。
可以通过对方程进行变形，用一个变量表示另一个变量，然后找出所有可能的正整数解。
将方程$2y + x = 7$变形为$x = 7 - 2y$。
由于$x$和$y$都需要是正整数，因此$7 - 2y$必须大于0，即$y$的取值范围在$1$到$3$之间（因为当$y=4$时，$x$将为负数，不满足正整数的条件）。
分别代入$y=1, 2, 3$进行计算。
【答案】：
当$y = 1$时，代入$x = 7 - 2y$，得$x = 7 - 2 × 1 = 5$；
当$y = 2$时，代入$x = 7 - 2y$，得$x = 7 - 2 × 2 = 3$；
当$y = 3$时，代入$x = 7 - 2y$，得$x = 7 - 2 × 3 = 1$；
综上，方程$2y + x = 7$的正整数解为：
$\begin{cases}x = 5, \\y = 1.\end{cases}$
$\begin{cases}x = 3, \\y = 2.\end{cases}$
$\begin{cases}x = 1, \\y = 3.\end{cases}$