2025年假期园地暑假作业七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期园地暑假作业七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列说法中正确的有( )
①$-64的立方根是-4$;②$49的算术平方根是\pm 7$;③$\frac{1}{27}的立方根是\frac{1}{3}$;④$\frac{1}{16}的平方根是\frac{1}{4}$.
A.$4$个
B.$3$个
C.$2$个
D.$1$个
①$-64的立方根是-4$;②$49的算术平方根是\pm 7$;③$\frac{1}{27}的立方根是\frac{1}{3}$;④$\frac{1}{16}的平方根是\frac{1}{4}$.
A.$4$个
B.$3$个
C.$2$个
D.$1$个
答案:
C
2. 估计$78$的立方根在( )
A.$2与3$之间
B.$3与4$之间
C.$4与5$之间
D.$5与6$之间
A.$2与3$之间
B.$3与4$之间
C.$4与5$之间
D.$5与6$之间
答案:
C
3. 若$(a + 1)^2与\sqrt{a + b - 8}$互为相反数,则$\sqrt[3]{ab}$的值为( )
A.$3$
B.$-3$
C.$\sqrt[3]{9}$
D.$-\sqrt[3]{9}$
A.$3$
B.$-3$
C.$\sqrt[3]{9}$
D.$-\sqrt[3]{9}$
答案:
D
4. 若$\sqrt{x - 1} - \sqrt{1 - x} = (x + y)^2$,则$x - y$的值为( )
A.$-1$
B.$1$
C.$2$
D.$3$
A.$-1$
B.$1$
C.$2$
D.$3$
答案:
C
5. 如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的正方形的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点$A$处,则点$A$表示的数是( )
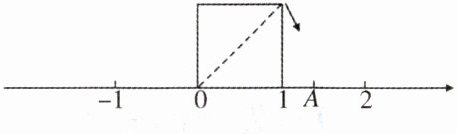
A.$1\frac{1}{2}$
B.$1.4$
C.$\sqrt{3}$
D.$\sqrt{2}$

A.$1\frac{1}{2}$
B.$1.4$
C.$\sqrt{3}$
D.$\sqrt{2}$
答案:
D
6. 实数$64$的立方根是______.
答案:
4
7. 写出一个大于$2且小于3$的无理数:______.
答案:
$\sqrt{5}$
8. 点$A在数轴上和表示1的点相距\sqrt{6}$个单位长度,则$A$表示的数为______.
答案:
$1-\sqrt{6}$或$1+\sqrt{6}$
9. 若$x$,$y$为实数,且$|x + 2| + \sqrt{y - 3} = 0$,则$(x + y)^{2010}$的值为______.
答案:
1
10. 如图,在平面直角坐标系中,直线$AB交x轴于A$点,交$y轴于B$点,点$C是直线AB$上一动点.
(1)若$\angle OAB比\angle OBA大20^{\circ}$,$OC\perp AB$,求$\angle AOC$的度数.
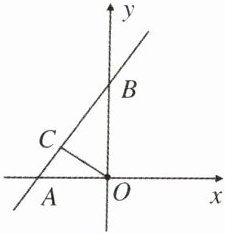
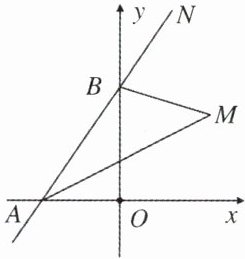
(2)点$N为AB$延长线上一点,$AM平分\angle BAO$,$BM平分\angle OBN$,当$A点在x$轴负半轴上运动时,$\angle AMB$的值是否发生变化?若不变,求出$\angle AMB$的度数;若变化,请说明理由.
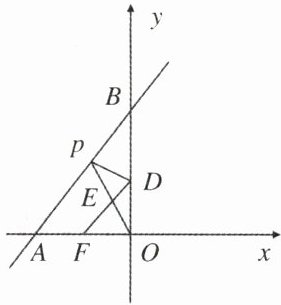
(3)沿$AB$,$OB$放置两面镜子,从$O点发出的光线经AB$,$OB$两次反射后,反射光线$DF与入射光线OP交于E$点. 若$\angle OAB = 45^{\circ}$,下列两个结论:①$DF// AB$,②$DF\perp OP$,其中有且只有一个结论是正确的,请你指出正确的结论,并说明理由.
(1)若$\angle OAB比\angle OBA大20^{\circ}$,$OC\perp AB$,求$\angle AOC$的度数.

(2)点$N为AB$延长线上一点,$AM平分\angle BAO$,$BM平分\angle OBN$,当$A点在x$轴负半轴上运动时,$\angle AMB$的值是否发生变化?若不变,求出$\angle AMB$的度数;若变化,请说明理由.

(3)沿$AB$,$OB$放置两面镜子,从$O点发出的光线经AB$,$OB$两次反射后,反射光线$DF与入射光线OP交于E$点. 若$\angle OAB = 45^{\circ}$,下列两个结论:①$DF// AB$,②$DF\perp OP$,其中有且只有一个结论是正确的,请你指出正确的结论,并说明理由.

答案:
(1)$\angle AOC=35^{\circ}$;
(2)$\angle AMB$的值不变,理由如下:$\angle AMB=\angle NBM-\angle BAM$,
$\angle NBM=\frac{1}{2}\angle NBO=\frac{1}{2}(\angle BAO+\angle AOB)$,$\angle BAM=$$\frac{1}{2}\angle BAO$,所以$\angle AMB=\frac{1}{2}\angle AOB=45^{\circ}$;
(3)结论②是正确的.
设$\angle APO=\alpha$,则$\angle BPD=\alpha$,所以$\angle DPO=180^{\circ}-2\alpha$.
因为$\angle OAB=45^{\circ}$,$\angle AOB=90^{\circ}$,所以$\angle ABO=45^{\circ}$.
$\angle ODF=\angle BDP=135^{\circ}-\alpha$,所以$\angle PDE=180^{\circ}-2(135^{\circ}-$$\alpha )=2\alpha -90^{\circ}$.
所以$\angle DPO+\angle PDE=180^{\circ}-2\alpha +2\alpha -90^{\circ}=90^{\circ}$.所以DF$\perp OP$.
(2)$\angle AMB$的值不变,理由如下:$\angle AMB=\angle NBM-\angle BAM$,
$\angle NBM=\frac{1}{2}\angle NBO=\frac{1}{2}(\angle BAO+\angle AOB)$,$\angle BAM=$$\frac{1}{2}\angle BAO$,所以$\angle AMB=\frac{1}{2}\angle AOB=45^{\circ}$;
(3)结论②是正确的.
设$\angle APO=\alpha$,则$\angle BPD=\alpha$,所以$\angle DPO=180^{\circ}-2\alpha$.
因为$\angle OAB=45^{\circ}$,$\angle AOB=90^{\circ}$,所以$\angle ABO=45^{\circ}$.
$\angle ODF=\angle BDP=135^{\circ}-\alpha$,所以$\angle PDE=180^{\circ}-2(135^{\circ}-$$\alpha )=2\alpha -90^{\circ}$.
所以$\angle DPO+\angle PDE=180^{\circ}-2\alpha +2\alpha -90^{\circ}=90^{\circ}$.所以DF$\perp OP$.
查看更多完整答案,请扫码查看


