《2025年假期园地暑假作业七年级数学人教版》

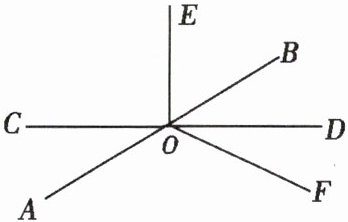
8. 如图,直线 $ AB $,$ CD $ 相交于点 $ O $,$ OD $ 平分 $ \angle BOF $,$ EO \perp CD $ 于点 $ O $,$ \angle EOF = 126 ^ { \circ } $,求 $ \angle COA $ 的度数。

答案： $\because EO \perp CD,\therefore \angle EOD=90^{\circ}.\therefore \angle DOF=\angle EOF-\angle EOD=126^{\circ}-90^{\circ}=36^{\circ}.$又$\because OD$平分$\angle BOF,\therefore \angle BOD=\angle DOF=36^{\circ}.$故由对顶角性质可知,$\angle COA=\angle BOD=36^{\circ}.$

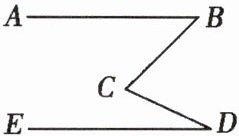
9. 如图,$ \angle BCD = \angle B + \angle D $,求证：$ AB // ED $。

答案： 证明:如图,过点C作$CF // AB$,所以$\angle 1=\angle B$,又因为$\angle BCD=\angle B+\angle D$,那么$\angle 1+\angle 2=\angle B+\angle D$,得$\angle 2=\angle D$,得$CF // ED$,所以$AB // ED.$

10. 如图,已知 $ AB // CD $,$ \angle AMP = 150 ^ { \circ } $,$ \angle PND = 60 ^ { \circ } $,请说明 $ MP \perp PN $ 的理由。

答案： 要说明$MP \perp PN$,即证$\angle MPN=90^{\circ}$,直接求证比较困难,需将$\angle MPN$分成两个角,可过P作$PH // AB$(图略),而$AB // CD$,所以$PH // CD$.$\therefore \angle AMP+\angle MPH=180^{\circ}$(两直线平行,同旁内角互补),而$\angle AMP=150^{\circ}$,$\therefore \angle MPH=180^{\circ}-150^{\circ}=30^{\circ}$,$\angle HPN=\angle PND=60^{\circ}$(两直线平行,内错角相等),$\therefore \angle MPN=\angle MPH+\angle HPN=30^{\circ}+60^{\circ}=90^{\circ}$,即$MP \perp PN.$