15. 在“探究影响滑动摩擦力大小的因素”的实验中,小潘同学选择了三块粗糙程度不同的长木板、一个木块、质量相等的钩码若干、一个弹簧测力计,进行实验。
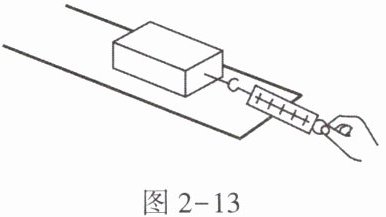
(1) 如图 2-13 所示,将木块放在水平长木板上,用弹簧测力计沿水平方向拉动木块,使其做____运动,根据____知识可知,木块受到的滑动摩擦力的大小等于弹簧测力计的示数。
(2) 小潘经过多次实验获得下表中的实验数据。
|实验次数|实验条件|弹簧测力计示数 F/N|
|----|----|----|
|1|木块|长木板|0.8|
|2|木块上放 1 个钩码|长木板|1.0|
|3|木块上放 2 个钩码|长木板|1.2|
|4|木块上放 1 个钩码|粗糙长木板|1.3|
|5|木块上放 1 个钩码|更粗糙长木板|1.7|
①分析表中____三次实验数据,可以得出结论:在接触面的粗糙程度相同的情况下,压力越大,滑动摩擦力越____。
②分析表中 2、4、5 三次实验数据,可以得出结论:在____相同的情况下,接触面越粗糙,滑动摩擦力越大。
(3) 实验过程中,当弹簧测力计的示数为 0.5N 时,木块未被拉动,此时木块受到的摩擦力____(选填“大于”“小于”或“等于”)0.5N。
(4) 体操运动员上器械前,会在手上涂防滑粉,这是通过增大____来增大摩擦的。
(1) 如图 2-13 所示,将木块放在水平长木板上,用弹簧测力计沿水平方向拉动木块,使其做____运动,根据____知识可知,木块受到的滑动摩擦力的大小等于弹簧测力计的示数。

(2) 小潘经过多次实验获得下表中的实验数据。
|实验次数|实验条件|弹簧测力计示数 F/N|
|----|----|----|
|1|木块|长木板|0.8|
|2|木块上放 1 个钩码|长木板|1.0|
|3|木块上放 2 个钩码|长木板|1.2|
|4|木块上放 1 个钩码|粗糙长木板|1.3|
|5|木块上放 1 个钩码|更粗糙长木板|1.7|
①分析表中____三次实验数据,可以得出结论:在接触面的粗糙程度相同的情况下,压力越大,滑动摩擦力越____。
②分析表中 2、4、5 三次实验数据,可以得出结论:在____相同的情况下,接触面越粗糙,滑动摩擦力越大。
(3) 实验过程中,当弹簧测力计的示数为 0.5N 时,木块未被拉动,此时木块受到的摩擦力____(选填“大于”“小于”或“等于”)0.5N。
(4) 体操运动员上器械前,会在手上涂防滑粉,这是通过增大____来增大摩擦的。
答案:
【解析】:
(1) 用弹簧测力计沿水平方向拉动木块,使其做匀速直线运动,根据二力平衡知识可知,木块受到的滑动摩擦力的大小等于弹簧测力计的示数。
(2) ①分析表中1、2、3三次实验数据,接触面粗糙程度相同,压力不同,弹簧测力计示数不同,即滑动摩擦力不同,可以得出结论:在接触面的粗糙程度相同的情况下,压力越大,滑动摩擦力越大。
②分析表中2、4、5三次实验数据,压力相同,接触面粗糙程度不同,弹簧测力计示数不同,即滑动摩擦力不同,可以得出结论:在压力相同的情况下,接触面越粗糙,滑动摩擦力越大。
(3) 实验过程中,当弹簧测力计的示数为$0.5N$时,木块未被拉动,木块处于静止状态,受到平衡力作用,此时木块受到的摩擦力等于拉力$0.5N$。
(4) 体操运动员上器械前,会在手上涂防滑粉,这是通过增大接触面的粗糙程度来增大摩擦的。
【答案】:
(1) 匀速直线;二力平衡
(2) ①1、2、3;大 ②压力
(3) 等于
(4) 接触面的粗糙程度
(1) 用弹簧测力计沿水平方向拉动木块,使其做匀速直线运动,根据二力平衡知识可知,木块受到的滑动摩擦力的大小等于弹簧测力计的示数。
(2) ①分析表中1、2、3三次实验数据,接触面粗糙程度相同,压力不同,弹簧测力计示数不同,即滑动摩擦力不同,可以得出结论:在接触面的粗糙程度相同的情况下,压力越大,滑动摩擦力越大。
②分析表中2、4、5三次实验数据,压力相同,接触面粗糙程度不同,弹簧测力计示数不同,即滑动摩擦力不同,可以得出结论:在压力相同的情况下,接触面越粗糙,滑动摩擦力越大。
(3) 实验过程中,当弹簧测力计的示数为$0.5N$时,木块未被拉动,木块处于静止状态,受到平衡力作用,此时木块受到的摩擦力等于拉力$0.5N$。
(4) 体操运动员上器械前,会在手上涂防滑粉,这是通过增大接触面的粗糙程度来增大摩擦的。
【答案】:
(1) 匀速直线;二力平衡
(2) ①1、2、3;大 ②压力
(3) 等于
(4) 接触面的粗糙程度
16. 一辆自重是 5.0×10⁴N 的卡车,装有 25 箱货物,每箱货物的质量是 300kg,行驶到一座立有限重标志(如图 2-14 所示)的桥前,问:
(1) 这辆卡车的总重力是多少?
(2) 该卡车要想安全过桥,至少需要卸下几箱货物? (g 取 10N/kg)

(1) 这辆卡车的总重力是多少?
(2) 该卡车要想安全过桥,至少需要卸下几箱货物? (g 取 10N/kg)

答案:
【解析】:
### (1)计算卡车的总重力
- 首先计算货物的总质量$m_{货}$:
已知每箱货物质量$m_{0}=300kg$,货物箱数$n = 25$,根据$m_{货}=n\times m_{0}$,可得$m_{货}=25\times300kg = 7500kg$。
再根据$G = mg$($g = 10N/kg$)计算货物的总重力$G_{货}$,$G_{货}=m_{货}g=7500kg\times10N/kg = 7.5\times10^{4}N$。
- 然后计算卡车的总重力$G_{总}$:
已知卡车自重$G_{车}=5.0\times10^{4}N$,根据$G_{总}=G_{车}+G_{货}$,可得$G_{总}=5.0\times10^{4}N + 7.5\times10^{4}N=1.25\times10^{5}N$。
### (2)计算至少需要卸下的货物箱数
- 先计算卡车的总质量$m_{总}$:
由$G = mg$可得$m=\frac{G}{g}$,已知$G_{总}=1.25\times10^{5}N$,$g = 10N/kg$,则$m_{总}=\frac{G_{总}}{g}=\frac{1.25\times10^{5}N}{10N/kg}=12500kg = 12.5t$。
- 再计算允许货物的质量$m_{允}$:
由限重标志知$m_{限}=10t = 10000kg$,则允许货物的质量$m_{允}=m_{限}-m_{车}$,卡车自重$m_{车}=\frac{G_{车}}{g}=\frac{5.0\times10^{4}N}{10N/kg}=5000kg$,所以$m_{允}=10000kg - 5000kg = 5000kg$。
- 最后计算至少卸下的货物箱数$n_{卸}$:
已装货物质量$m_{货}=7500kg$,则卸下货物质量$\Delta m=m_{货}-m_{允}=7500kg - 5000kg = 2500kg$。
每箱货物质量$m_{0}=300kg$,则$n_{卸}=\frac{\Delta m}{m_{0}}=\frac{2500kg}{300kg}\approx 9$(箱)(这里采用进一法,因为$8$箱卸下后还超重)。
【答案】:
(1) $1.25\times10^{5}N$;
(2) $9$箱
### (1)计算卡车的总重力
- 首先计算货物的总质量$m_{货}$:
已知每箱货物质量$m_{0}=300kg$,货物箱数$n = 25$,根据$m_{货}=n\times m_{0}$,可得$m_{货}=25\times300kg = 7500kg$。
再根据$G = mg$($g = 10N/kg$)计算货物的总重力$G_{货}$,$G_{货}=m_{货}g=7500kg\times10N/kg = 7.5\times10^{4}N$。
- 然后计算卡车的总重力$G_{总}$:
已知卡车自重$G_{车}=5.0\times10^{4}N$,根据$G_{总}=G_{车}+G_{货}$,可得$G_{总}=5.0\times10^{4}N + 7.5\times10^{4}N=1.25\times10^{5}N$。
### (2)计算至少需要卸下的货物箱数
- 先计算卡车的总质量$m_{总}$:
由$G = mg$可得$m=\frac{G}{g}$,已知$G_{总}=1.25\times10^{5}N$,$g = 10N/kg$,则$m_{总}=\frac{G_{总}}{g}=\frac{1.25\times10^{5}N}{10N/kg}=12500kg = 12.5t$。
- 再计算允许货物的质量$m_{允}$:
由限重标志知$m_{限}=10t = 10000kg$,则允许货物的质量$m_{允}=m_{限}-m_{车}$,卡车自重$m_{车}=\frac{G_{车}}{g}=\frac{5.0\times10^{4}N}{10N/kg}=5000kg$,所以$m_{允}=10000kg - 5000kg = 5000kg$。
- 最后计算至少卸下的货物箱数$n_{卸}$:
已装货物质量$m_{货}=7500kg$,则卸下货物质量$\Delta m=m_{货}-m_{允}=7500kg - 5000kg = 2500kg$。
每箱货物质量$m_{0}=300kg$,则$n_{卸}=\frac{\Delta m}{m_{0}}=\frac{2500kg}{300kg}\approx 9$(箱)(这里采用进一法,因为$8$箱卸下后还超重)。
【答案】:
(1) $1.25\times10^{5}N$;
(2) $9$箱
查看更多完整答案,请扫码查看


