《2025年暑假作业本大象出版社八年级物理北师大版》

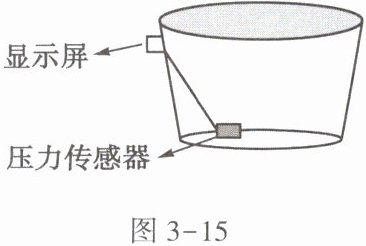
18. 为解决山区缺水问题,一些农户修建了水窖,在雨季将雨水收集到水窖中,以备干旱季节使用。小明家也修建了这样一个水窖,形状如图3-15所示。为便于观察储水情况,小明在水窖底部安装了一个压力传感器,压力大小在显示屏上显示,压力大表示水窖中的水较____。用水过程中发现,虽然每天用水量基本相同,但每天压力大小下降却不相同,而且随着储水量的减少,下降得越来越快,出现该现象的原因是____。

答案： 【解析】：根据$p = \rho gh$（$\rho$为液体密度，$g$为重力加速度，$h$为深度），$F = pS$（$S$为受力面积），压力传感器受到的压力$F=\rho ghS$，在$\rho$、$g$、$S$不变时，压力$F$越大，说明水的深度$h$越大，即水窖中的水较深。
水窖上粗下细，每天用水量基本相同（即体积变化$\Delta V$相同），根据$h=\frac{V}{S}$（$V$为体积，$S$为横截面积），随着储水量减少，水窖横截面积$S$变小，相同体积变化量$\Delta V$对应的深度变化量$\Delta h$越大，再根据$F = pS=\rho ghS$（$\rho$、$g$、$S$不变时），压力变化$\Delta F=\rho gS\Delta h$，所以压力下降越来越快。
【答案】：深；水窖上粗下细，相同体积的水，水越少，水的深度减小得越快，由$F = pS=\rho ghS$（$\rho$、$g$、$S$不变时）可知压力下降就越快

19. 如图3-16所示,高压锅的锅盖上有一个空心柱(排气孔),空心柱上“戴”着一个帽子(限压阀)。当高压锅内气体的压强超过安全值时,其内的气体就会冲出限压阀,排出一部分,使锅内气体的压强减小。现有一个直径为24 cm、空心柱小孔的横截面积为$10mm^{2}$、限压阀质量为100 g的高压锅,要用它来煮饭,已知当时的大气压为$1.0×10^{5}Pa$。(g取10 N/kg)
(1)此高压锅内气体能达到的最大压强是多少?
(2)商品质量检测部门要求,此高压锅内气体的最大压强不能超过$1.8×10^{5}Pa$。为使此高压锅能继续安全使用,原来的限压阀还能使用吗?若不能,应再配备一个质量为多少克的限压阀?

答案： 【解析】：
### （1）计算高压锅内气体能达到的最大压强
- 首先计算限压阀的重力$G = mg$，已知$m = 100g=0.1kg$，$g = 10N/kg$，则$G=0.1kg\times10N/kg = 1N$。
- 空心柱小孔的横截面积$S = 10mm^{2}=10\times10^{- 6}m^{2}=1\times10^{-5}m^{2}$。
- 限压阀对出气孔产生的压强$p_{阀}=\frac{F}{S}=\frac{G}{S}$，将$G = 1N$，$S = 1\times10^{-5}m^{2}$代入可得$p_{阀}=\frac{1N}{1\times10^{-5}m^{2}}=1\times10^{5}Pa$。
- 锅内气体能达到的最大压强$p = p_{0}+p_{阀}$，已知$p_{0}=1.0\times10^{5}Pa$，所以$p = 1.0\times10^{5}Pa+1\times10^{5}Pa=2\times10^{5}Pa$。
### （2）判断原来限压阀能否使用并计算合适限压阀质量
已知商品质量检测部门要求锅内气体最大压强$p'=1.8\times10^{5}Pa$，则限压阀需要产生的压强$p_{阀}'=p'-p_{0}$，$p_{0}=1.0\times10^{5}Pa$，所以$p_{阀}'=1.8\times10^{5}Pa - 1.0\times10^{5}Pa=0.8\times10^{5}Pa$。
由$p=\frac{F}{S}$可得限压阀的重力$G'=F'=p_{阀}'S$，$p_{阀}'=0.8\times10^{5}Pa$，$S = 1\times10^{-5}m^{2}$，则$G'=0.8\times10^{5}Pa\times1\times10^{-5}m^{2}=0.8N$。
再由$G = mg$可得限压阀质量$m'=\frac{G'}{g}$，$g = 10N/kg$，所以$m'=\frac{0.8N}{10N/kg}=0.08kg = 80g$。
因为$2\times10^{5}Pa＞1.8\times10^{5}Pa$，所以原来的限压阀不能使用。
【答案】：
(1) $2\times10^{5}Pa$
(2) 原来的限压阀不能使用，应配备一个质量为$\boldsymbol{80g}$的限压阀。