2025年暑假乐园海南出版社四年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假乐园海南出版社四年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
画直线,找规律
经过2个点,可以画1条直线;经过不在同一条直线上的3个点中的每两个点画直线,最多可以画3条直线;经过4个点中的每两个点呢?5个点、6个点或更多个点呢?
请你画一画、数一数,找一找其中的规律。
这是一个十分有趣的问题,我画了数,数了又画,经过几次试验,终于发现了其中的规律:
|点数|直线条数|规律|
|----|----|----|
|2|1|$(2 - 1)$即1|
|3|3|$1 + (3 - 1)$即$1 + 2$|
|4|6|$1 + 2 + (4 - 1)$即$1 + 2 + 3$|
|5|10|$1 + 2 + 3 + (5 - 1)$即$1 + 2 + 3 + 4$|
|6|15|$1 + 2 + 3 + 4 + (6 - 1)$即$1 + 2 + 3 + 4 + 5$|
|……|……|……|
必须说明的是,要使画出的直线最多,就得保证这些点中的任意三点均不在同一条直线上。
同学们,你们说我发现的这个规律正确吗?验算一下,说不定你也会有新的发现呢。
经过2个点,可以画1条直线;经过不在同一条直线上的3个点中的每两个点画直线,最多可以画3条直线;经过4个点中的每两个点呢?5个点、6个点或更多个点呢?
请你画一画、数一数,找一找其中的规律。
这是一个十分有趣的问题,我画了数,数了又画,经过几次试验,终于发现了其中的规律:
|点数|直线条数|规律|
|----|----|----|
|2|1|$(2 - 1)$即1|
|3|3|$1 + (3 - 1)$即$1 + 2$|
|4|6|$1 + 2 + (4 - 1)$即$1 + 2 + 3$|
|5|10|$1 + 2 + 3 + (5 - 1)$即$1 + 2 + 3 + 4$|
|6|15|$1 + 2 + 3 + 4 + (6 - 1)$即$1 + 2 + 3 + 4 + 5$|
|……|……|……|
必须说明的是,要使画出的直线最多,就得保证这些点中的任意三点均不在同一条直线上。
同学们,你们说我发现的这个规律正确吗?验算一下,说不定你也会有新的发现呢。
答案:
【解析】:我们来分析这个规律的推导过程。设点的个数为$n$($n\geqslant2$且$n$为整数),当有$2$个点时,只能画$1$条直线,即$1=\frac{2\times(2 - 1)}{2}$;当有$3$个点时,从第一个点出发可以和另外$2$个点画$2$条直线,从第二个点出发(因为和第一个点已经连过了)可以和第三个点画$1$条直线,总共$2 + 1=3$条直线,即$3=\frac{3\times(3 - 1)}{2}$;当有$4$个点时,从第一个点出发可以和另外$3$个点画$3$条直线,从第二个点出发可以和除第一个点外的另外$2$个点画$2$条直线,从第三个点出发可以和除前两个点外的第四个点画$1$条直线,总共$3+2 + 1 = 6$条直线,即$6=\frac{4\times(4 - 1)}{2}$;以此类推,当有$n$个点时,最多可画直线的条数为$1 + 2+3+\cdots+(n - 1)$,根据等差数列求和公式$S=\frac{n\times(n - 1)}{2}$(这里首项$a_1 = 1$,末项$a_{n-1}=n - 1$,项数为$n - 1$)。所以题目中总结的规律“经过$n$个点(任意三点均不在同一条直线上)中的每两个点画直线,最多可画直线的条数为$1+2+\cdots+(n - 1)$”是正确的。
【答案】:这个规律是正确的。
【答案】:这个规律是正确的。
有一块地(如图),要平均分给5户人家,要求形状一样、大小相同。你会分割吗?
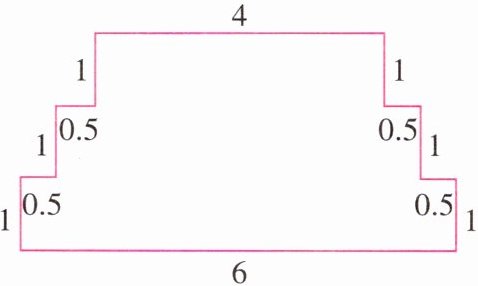

答案:
【解析】:先计算这块地的总面积,通过分割图形计算。把这块地看作一个大长方形减去几个小长方形。大长方形长$6$,宽$1 + 1+1=3$,面积为$6×3 = 18$,减去的小长方形部分:两个长$1$宽$0.5$的小长方形面积为$2×(1×0.5)=1$,两个长$(1 + 1)$宽$0.5$的小长方形面积为$2×(2×0.5)=2$,总面积是$18-1 - 2=15$。平均分给$5$户人家,每户面积是$15÷5 = 3$。
观察图形的特点,从左到右或从右到左进行分割,因为图形左右对称。可以将图形沿着横向和纵向进行分割,由于图形的高度方向有$3$个$1$的长度,宽度方向通过计算和尝试,发现可以把图形分割成$5$个形状为直角梯形的部分。
从左边开始,第一个直角梯形:上底$1$,下底$2$,高$2$,根据梯形面积公式$S=(a + b)h÷2$,$(1 + 2)×2÷2=3$。按照这样的方法依次对整个图形进行分割(具体分割线根据梯形的定义和面积要求确定,利用图形的对称性和边长关系)。
【答案】:可以将这块地分割成$5$个形状为直角梯形(上底$1$,下底$2$,高$2$)的部分(具体分割线根据图形对称性和边长关系画出)。
观察图形的特点,从左到右或从右到左进行分割,因为图形左右对称。可以将图形沿着横向和纵向进行分割,由于图形的高度方向有$3$个$1$的长度,宽度方向通过计算和尝试,发现可以把图形分割成$5$个形状为直角梯形的部分。
从左边开始,第一个直角梯形:上底$1$,下底$2$,高$2$,根据梯形面积公式$S=(a + b)h÷2$,$(1 + 2)×2÷2=3$。按照这样的方法依次对整个图形进行分割(具体分割线根据梯形的定义和面积要求确定,利用图形的对称性和边长关系)。
【答案】:可以将这块地分割成$5$个形状为直角梯形(上底$1$,下底$2$,高$2$)的部分(具体分割线根据图形对称性和边长关系画出)。
查看更多完整答案,请扫码查看


