2025年暑假乐园海南出版社四年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假乐园海南出版社四年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
一、作业很简单,快乐算一算。
$379×0=$ $45+0÷7=$ $6×8-42=$ $580+0=$
$40×3÷6=$ $(40-0)×9=$ $6000-0=$ $45+8-32=$
$0×(25+47)=$ $0÷200=$ $60-50÷5=$ $15×(16÷8)=$
$379×0=$ $45+0÷7=$ $6×8-42=$ $580+0=$
$40×3÷6=$ $(40-0)×9=$ $6000-0=$ $45+8-32=$
$0×(25+47)=$ $0÷200=$ $60-50÷5=$ $15×(16÷8)=$
答案:
【解析】:
1. 对于$379×0$:根据任何数乘以$0$都得$0$,所以$379×0 = 0$。
2. 对于$45 + 0÷7$:先算除法,$0$除以任何非零数都得$0$,即$0÷7 = 0$,再算加法$45+0 = 45$。
3. 对于$6×8 - 42$:先算乘法$6×8 = 48$,再算减法$48 - 42 = 6$。
4. 对于$580 + 0$:任何数加$0$都等于它本身,所以$580+0 = 580$。
5. 对于$40×3÷6$:按照从左到右的顺序计算,先算$40×3 = 120$,再算$120÷6 = 20$。
6. 对于$(40 - 0)×9$:先算括号里的$40 - 0 = 40$,再算乘法$40×9 = 360$。
7. 对于$6000 - 0$:任何数减$0$都等于它本身,所以$6000 - 0 = 6000$。
8. 对于$45 + 8 - 32$:按照从左到右的顺序计算,先算$45+8 = 53$,再算$53 - 32 = 21$。
9. 对于$0×(25 + 47)$:先算括号里的$25 + 47 = 72$,再算乘法$0×72 = 0$。
10. 对于$0÷200$:$0$除以任何非零数都得$0$,所以$0÷200 = 0$。
11. 对于$60 - 50÷5$:先算除法$50÷5 = 10$,再算减法$60 - 10 = 50$。
12. 对于$15×(16÷8)$:先算括号里的$16÷8 = 2$,再算乘法$15×2 = 30$。
【答案】:$0$;$45$;$6$;$580$;$20$;$360$;$6000$;$21$;$0$;$0$;$50$;$30$
1. 对于$379×0$:根据任何数乘以$0$都得$0$,所以$379×0 = 0$。
2. 对于$45 + 0÷7$:先算除法,$0$除以任何非零数都得$0$,即$0÷7 = 0$,再算加法$45+0 = 45$。
3. 对于$6×8 - 42$:先算乘法$6×8 = 48$,再算减法$48 - 42 = 6$。
4. 对于$580 + 0$:任何数加$0$都等于它本身,所以$580+0 = 580$。
5. 对于$40×3÷6$:按照从左到右的顺序计算,先算$40×3 = 120$,再算$120÷6 = 20$。
6. 对于$(40 - 0)×9$:先算括号里的$40 - 0 = 40$,再算乘法$40×9 = 360$。
7. 对于$6000 - 0$:任何数减$0$都等于它本身,所以$6000 - 0 = 6000$。
8. 对于$45 + 8 - 32$:按照从左到右的顺序计算,先算$45+8 = 53$,再算$53 - 32 = 21$。
9. 对于$0×(25 + 47)$:先算括号里的$25 + 47 = 72$,再算乘法$0×72 = 0$。
10. 对于$0÷200$:$0$除以任何非零数都得$0$,所以$0÷200 = 0$。
11. 对于$60 - 50÷5$:先算除法$50÷5 = 10$,再算减法$60 - 10 = 50$。
12. 对于$15×(16÷8)$:先算括号里的$16÷8 = 2$,再算乘法$15×2 = 30$。
【答案】:$0$;$45$;$6$;$580$;$20$;$360$;$6000$;$21$;$0$;$0$;$50$;$30$
二、有344本故事书,每个班分24本,可以分给多少个班?
下面是小红计算的竖式,竖式中箭头所指的数表示的意思是()
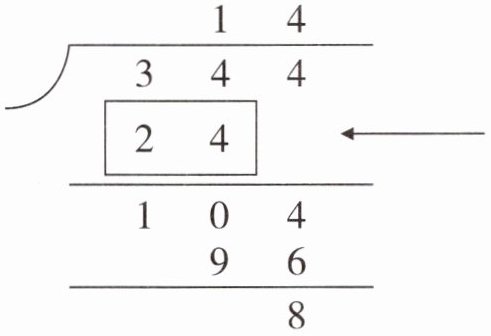
A. 先分掉24本
B. 先分掉240本
C. 每班分到24本
D. 每班分到240本
下面是小红计算的竖式,竖式中箭头所指的数表示的意思是()

A. 先分掉24本
B. 先分掉240本
C. 每班分到24本
D. 每班分到240本
答案:
B
三、用竖式计算。
$708×36$ $780×36$ $435÷35$
$708×36$ $780×36$ $435÷35$
答案:
【解析】:
计算$708×36$时,先用$36$个位上的$6$去乘$708$,$6×708 = 4248$,再用$36$十位上的$3$去乘$708$,$30×708 = 21240$,最后将两次乘得的积相加,$4248+21240 = 25488$。
计算$780×36$时,可先计算$78×36$,先用$36$个位上的$6$去乘$78$,$6×78 = 468$,再用$36$十位上的$3$去乘$78$,$30×78 = 2340$,$468 + 2340=2808$,因为因数$780$末尾有一个$0$,所以在$2808$后面添上一个$0$,结果是$28080$。
计算$435÷35$时,先看被除数的前两位$43$,$43\gt35$,所以商是两位数,$43$里面最多有$1$个$35$,商$1$写在十位上,$43 - 35 = 8$,再把个位上的$5$落下来,$85$里面最多有$2$个$35$,商$2$写在个位上,$85-70 = 15$,所以$435÷35 = 12\cdots\cdots15$。
【答案】:$708×36 = 25488$;$780×36 = 28080$;$435÷35 = 12\cdots\cdots15$
计算$708×36$时,先用$36$个位上的$6$去乘$708$,$6×708 = 4248$,再用$36$十位上的$3$去乘$708$,$30×708 = 21240$,最后将两次乘得的积相加,$4248+21240 = 25488$。
计算$780×36$时,可先计算$78×36$,先用$36$个位上的$6$去乘$78$,$6×78 = 468$,再用$36$十位上的$3$去乘$78$,$30×78 = 2340$,$468 + 2340=2808$,因为因数$780$末尾有一个$0$,所以在$2808$后面添上一个$0$,结果是$28080$。
计算$435÷35$时,先看被除数的前两位$43$,$43\gt35$,所以商是两位数,$43$里面最多有$1$个$35$,商$1$写在十位上,$43 - 35 = 8$,再把个位上的$5$落下来,$85$里面最多有$2$个$35$,商$2$写在个位上,$85-70 = 15$,所以$435÷35 = 12\cdots\cdots15$。
【答案】:$708×36 = 25488$;$780×36 = 28080$;$435÷35 = 12\cdots\cdots15$
四、你能根据$18×2=36$,直接写出下面算式的积吗?
$18×20=$ $180×2=$ $180×20=$
$18×200=$ $1800×2=$ $1800×20=$
请你分享快速求出其他算式的积的秘诀。
$18×20=$ $180×2=$ $180×20=$
$18×200=$ $1800×2=$ $1800×20=$
请你分享快速求出其他算式的积的秘诀。
答案:
【解析】:根据积的变化规律来求解。积的变化规律为:在乘法算式中,一个因数不变,另一个因数扩大或缩小若干倍($0$除外),积就扩大或缩小相同的倍数;如果两个因数都扩大,那么积扩大的倍数就等于两个因数扩大倍数的乘积。
对于$18×20$,与$18×2 = 36$相比,一个因数$18$不变,另一个因数$2$扩大了$10$倍变为$20$,所以积也扩大$10$倍,$36×10 = 360$;
对于$180×2$,与$18×2 = 36$相比,一个因数$2$不变,另一个因数$18$扩大了$10$倍变为$180$,所以积也扩大$10$倍,$36×10 = 360$;
对于$180×20$,与$18×2 = 36$相比,一个因数$18$扩大了$10$倍变为$180$,另一个因数$2$扩大了$10$倍变为$20$,那么积扩大$10×10 = 100$倍,$36×100 = 3600$;
对于$18×200$,与$18×2 = 36$相比,一个因数$18$不变,另一个因数$2$扩大了$100$倍变为$200$,所以积也扩大$100$倍,$36×100 = 3600$;
对于$1800×2$,与$18×2 = 36$相比,一个因数$2$不变,另一个因数$18$扩大了$100$倍变为$1800$,所以积也扩大$100$倍,$36×100 = 3600$;
对于$1800×20$,与$18×2 = 36$相比,一个因数$18$扩大了$100$倍变为$1800$,另一个因数$2$扩大了$10$倍变为$20$,那么积扩大$100×10 = 1000$倍,$36×1000 = 36000$。
快速求出其他算式积的秘诀就是:先看与已知算式相比,因数分别扩大了多少倍,然后将已知算式的积乘以因数扩大倍数的乘积,就可以得到新算式的积。
【答案】:$360$;$360$;$3600$;$3600$;$3600$;$36000$
对于$18×20$,与$18×2 = 36$相比,一个因数$18$不变,另一个因数$2$扩大了$10$倍变为$20$,所以积也扩大$10$倍,$36×10 = 360$;
对于$180×2$,与$18×2 = 36$相比,一个因数$2$不变,另一个因数$18$扩大了$10$倍变为$180$,所以积也扩大$10$倍,$36×10 = 360$;
对于$180×20$,与$18×2 = 36$相比,一个因数$18$扩大了$10$倍变为$180$,另一个因数$2$扩大了$10$倍变为$20$,那么积扩大$10×10 = 100$倍,$36×100 = 3600$;
对于$18×200$,与$18×2 = 36$相比,一个因数$18$不变,另一个因数$2$扩大了$100$倍变为$200$,所以积也扩大$100$倍,$36×100 = 3600$;
对于$1800×2$,与$18×2 = 36$相比,一个因数$2$不变,另一个因数$18$扩大了$100$倍变为$1800$,所以积也扩大$100$倍,$36×100 = 3600$;
对于$1800×20$,与$18×2 = 36$相比,一个因数$18$扩大了$100$倍变为$1800$,另一个因数$2$扩大了$10$倍变为$20$,那么积扩大$100×10 = 1000$倍,$36×1000 = 36000$。
快速求出其他算式积的秘诀就是:先看与已知算式相比,因数分别扩大了多少倍,然后将已知算式的积乘以因数扩大倍数的乘积,就可以得到新算式的积。
【答案】:$360$;$360$;$3600$;$3600$;$3600$;$36000$
查看更多完整答案,请扫码查看


