《2025年暑假生活五年级B版重庆出版社》

3. 看图列方程解答。

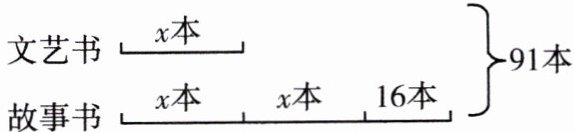
解：设文艺书有$x$本，故事书有$(2x + 16)$本。
$x+(2x + 16)=91$
$x+2x+16 = 91$
$3x+16 = 91$
$3x=91 - 16$
$3x=75$
$x = 75÷3$
$x=$25

答案： 【解析】：
已知文艺书有$x$本，故事书有$(2x + 16)$本，两种书一共有$91$本，可列方程：
$x+(2x + 16)=91$
$x+2x+16 = 91$
$3x+16 = 91$
$3x=91 - 16$
$3x=75$
$x = 75÷3$
$x = 25$
【答案】：$x = 25$

4. 学校买了15个足球,比买的排球少8个,已知每个足球60元,是排球单价的1.5倍。(先提一个数学问题,再列方程解答)

答案： 【解析】：本题可提出问题“买排球一共花了多少钱”。首先根据已知条件求出排球的个数和单价，设买排球一共花了$x$元，根据“总价$÷$数量$=$单价”的关系来列方程求解。
已知学校买了$15$个足球，比买的排球少$8$个，那么排球的个数为$15 + 8 = 23$个；又已知每个足球$60$元，是排球单价的$1.5$倍，则排球的单价为$60÷1.5 = 40$元。
根据上述分析可列方程$x÷23 = 40$，解方程：
$x÷23 = 40$
$x = 40×23$
$x = 920$
【答案】：买排球一共花了多少钱；920元

5. 数学活动课上,我们已经知道：两个偶数的和是一个偶数。现在,我们用“字母表示数”的方法来验证：
设这两个偶数为2m和2n(其中m、n都是整数),则它们的和为2m+2n= 2(m+n)。因为m、n都是整数,所以m+n也是整数。所以2(m+n)就是偶数,即两个偶数的和是一个偶数。
你会用上述方法说明“两个奇数的和是一个偶数”吗？

答案： 【解析】：设这两个奇数为$2m + 1$和$2n+1$（其中$m$、$n$都是整数），则它们的和为$(2m + 1)+(2n + 1)=2m+2n + 2=2(m + n + 1)$。因为$m$、$n$都是整数，所以$m + n+1$也是整数。所以$2(m + n + 1)$就是偶数，即两个奇数的和是一个偶数。
【答案】：设这两个奇数为$2m + 1$和$2n + 1$（$m$、$n$为整数），它们的和为$(2m + 1)+(2n + 1)=2(m + n + 1)$，因为$m$、$n$为整数，所以$m + n + 1$为整数，所以$2(m + n + 1)$是偶数，即两个奇数的和是偶数。