《2025年暑假生活五年级B版重庆出版社》

2. 用小棒按照如下方式摆图形(图4)。

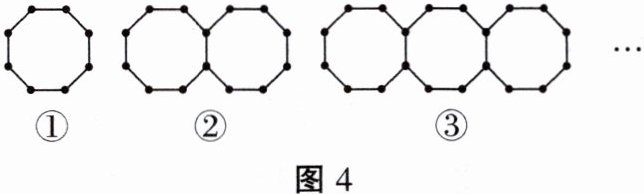
(1)按照上面的摆放方式,将下面的表格填写完整。（表格从左到右依次填入：22；29；36；7n + 1）
(2)2025根小棒能这样摆成多少个完整的八边形？289个

答案： 【解析】：
（1）观察图形规律，摆$1$个八边形用$8$根小棒；摆$2$个八边形时，相比摆$1$个八边形，第二个八边形与第一个八边形共用$1$根小棒，所以用$8 + 7=15$根小棒；摆$3$个八边形时，第三个八边形与第二个八边形共用$1$根小棒，所以用$8+7×2 = 22$根小棒；摆$4$个八边形时，用$8+7×3=29$根小棒；摆$5$个八边形时，用$8 + 7×4 = 36$根小棒；摆$n$个八边形时，用$8+7×(n - 1)=7n + 1$根小棒。
（2）设$2025$根小棒能摆成$x$个完整的八边形，根据（1）中得出的规律$7x+1 = 2025$，
$\begin{aligned}7x&=2025 - 1\\7x&=2024\\x&=2024÷7\\x&=289\cdots\cdots1\end{aligned}$
【答案】：
（1）$22$；$29$；$36$；$7n + 1$
（2）$289$个

四、善悟,看图并完成练习。
下面是张华和刘芳今年7次单元测验成绩表,请根据统计表,绘制折线统计图。
如果你是张华,看到这个折线统计图后会怎么做？
如果我是张华，看到这个折线统计图后，我会分析自己成绩的波动情况。比如第一次成绩89分相对较低，分析原因是知识点掌握不牢还是考试时粗心等。对于成绩稳定在95分左右的情况，总结好的学习方法继续保持。看到第六次成绩达到100分，分析这次考试成功的经验，比如对知识的全面掌握、良好的考试心态等。同时，对比刘芳的成绩，学习她成绩好的方面，比如她第三次成绩95分，看她在这一单元的学习方法有什么值得借鉴的地方。并且针对自己成绩波动的单元（如第三次成绩92分比第二次95分有所下降），查漏补缺，加强薄弱环节的学习。

答案： 1. 绘制折线统计图
- 首先，确定横纵坐标轴的含义，横坐标为单元，纵坐标为成绩（分）。
- 然后，根据张华的成绩$(89,95,92,95,95,100,95)$和刘芳的成绩$(90,92,95,92,92,99,92)$，在坐标图中依次描点。
- 最后，用实线连接张华的各点，用虚线连接刘芳的各点，并标注图例。
2. 张华的做法
如果我是张华，看到这个折线统计图后，我会分析自己成绩的波动情况。比如第一次成绩$89$分相对较低，分析原因是知识点掌握不牢还是考试时粗心等。对于成绩稳定在$95$分左右的情况，总结好的学习方法继续保持。看到第六次成绩达到$100$分，分析这次考试成功的经验，比如对知识的全面掌握、良好的考试心态等。同时，对比刘芳的成绩，学习她成绩好的方面，比如她第三次成绩$95$分，看她在这一单元的学习方法有什么值得借鉴的地方。并且针对自己成绩波动的单元（如第三次成绩$92$分比第二次$95$分有所下降），查漏补缺，加强薄弱环节的学习。
3. 放置星星问题
不能。因为图中一共有$6$行$6$列，每行每列星星数量均为偶数，那么星星总数应该是$6× k$（$k$为整数，表示每行星星数目的一半），总数是偶数。而现在已经有$7$颗星星（奇数），再放入$5$颗星星，$7 + 5=12$颗星星，$12÷6 = 2$，看似可以。但是从实际放置来看，通过尝试不同的放置方法，会发现无法满足每行每列星星数量均为偶数的要求（可以通过奇偶性原理和实际尝试来验证）。
综上，折线统计图按上述方法绘制；张华会分析成绩并改进学习；星星不能按要求放置。

2. 你能把另外五个星星放进格子里,使得每行每列的星星数量均为偶数吗？不能

答案： 解：
设格子为$6×6$的矩阵（假设图为$6×6$格子，根据一般此类题目设定）。
已知已有星星分布，设要放入的星星位置为$(x_{i},y_{i})$，$i = 1,2,3,4,5$。
根据每行每列星星数量为偶数的条件。
先看第一行，已有$1$个星星（奇数），要使第一行星星数为偶数，需再放$1$个星星（因为$1 + 1=2$（偶数））。
同理看第一列，已有$1$个星星（奇数），需再放$1$个星星。
假设在$(1,1)$位置放一个星星（第一行第一列）。
此时第一行有$2$个星星（偶数），第一列有$2$个星星（偶数）。
再看第二行，已有$2$个星星（偶数），若不再放星星，满足偶数条件，但总共要放$5$个星星，所以还需放。
假设在$(2,4)$位置放一个星星，此时第二行有$3$个星星（奇数），不满足，重新假设。
经过尝试（具体尝试过程：从第一行开始逐行逐列根据奇偶性条件去放置星星），发现无法完成。
因为：
从整体看，$6$行$6$列，每行每列星星数为偶数，则星星总数$N=\sum_{i = 1}^{6}a_{i}=\sum_{j = 1}^{6}b_{j}$（$a_{i}$表示第$i$行星星数，$b_{j}$表示第$j$列星星数），$N$必为偶数（因为$6$个偶数相加为偶数）。
而现在已有星星数（假设图中已有星星数为奇数，具体数可通过数图中星星得，假设为$9$个（奇数）），再放入$5$个星星，总数为$9 + 5=14$（偶数），但在放置过程中，由于行列相互制约（例如某一行满足偶数后，放置星星使某一列又变为奇数，且无法调整回来），所以不能把另外五个星星放进格子里，使得每行每列的星星数量均为偶数。
综上，不能。