2025年暑假集训合肥工业大学出版社五年级数学苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假集训合肥工业大学出版社五年级数学苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
知识点 1 5,2 和 3 的倍数的特征
例 1 一个三位数,同时是 2,3,5 的倍数,这个三位数最大是多少?
【解析】一个数同时是 2,3,5 的倍数,也就是同时具有 2,3,5 的倍数的特征:个位上是 0,且各位上的数的和是 3 的倍数。所以可以先确定个位上是 0。又因为要求的这个三位数最大,所以百位上最大可以是 9。根据 2、3、5 的倍数的特征可知:9 加十位上的数的和应是 3 的倍数,所以十位上最大可填 9。
【答案】990
例 1 一个三位数,同时是 2,3,5 的倍数,这个三位数最大是多少?
【解析】一个数同时是 2,3,5 的倍数,也就是同时具有 2,3,5 的倍数的特征:个位上是 0,且各位上的数的和是 3 的倍数。所以可以先确定个位上是 0。又因为要求的这个三位数最大,所以百位上最大可以是 9。根据 2、3、5 的倍数的特征可知:9 加十位上的数的和应是 3 的倍数,所以十位上最大可填 9。
【答案】990
答案:
【解析】
题目要求找出一个三位数,这个数需要同时是2、3、5的倍数。根据2、3、5的倍数的特征:
1. 一个数是2的倍数,其个位数字必须是偶数。
2. 一个数是3的倍数,其各位数字之和必须是3的倍数。
3. 一个数是5的倍数,其个位数字必须是0或5。
综合以上特征,个位数字只能是0(因为它是2和5的公倍数)。
为了得到最大的三位数,百位数字应尽可能大,即9。然后,需要确定十位数字,使得整个数是3的倍数。
已知百位是9,个位是0,设十位数字为$x$,则数字和为$9 + x + 0 = 9 + x$。
需要$9 + x$是3的倍数。
通过尝试0到9的数字,发现当$x = 9$时,$9 + 9 = 18$,18是3的倍数。
因此,满足条件的最大三位数是990。
【答案】
990
题目要求找出一个三位数,这个数需要同时是2、3、5的倍数。根据2、3、5的倍数的特征:
1. 一个数是2的倍数,其个位数字必须是偶数。
2. 一个数是3的倍数,其各位数字之和必须是3的倍数。
3. 一个数是5的倍数,其个位数字必须是0或5。
综合以上特征,个位数字只能是0(因为它是2和5的公倍数)。
为了得到最大的三位数,百位数字应尽可能大,即9。然后,需要确定十位数字,使得整个数是3的倍数。
已知百位是9,个位是0,设十位数字为$x$,则数字和为$9 + x + 0 = 9 + x$。
需要$9 + x$是3的倍数。
通过尝试0到9的数字,发现当$x = 9$时,$9 + 9 = 18$,18是3的倍数。
因此,满足条件的最大三位数是990。
【答案】
990
例 2 分一分。
2 3 6 9 17 20 1 18
【解析】判断一个数是质数还是合数,若找到 1 和它本身以外的一个因数,那么这个数就是合数。而质数只有 1 和它本身两个因数,所以比较好判断。
【答案】质数:2,3,17
合数:6,9,18,20
2 3 6 9 17 20 1 18

【解析】判断一个数是质数还是合数,若找到 1 和它本身以外的一个因数,那么这个数就是合数。而质数只有 1 和它本身两个因数,所以比较好判断。
【答案】质数:2,3,17
合数:6,9,18,20
答案:
解析:本题考查质数与合数的概念。质数是指在大于 1 的自然数中,除了 1 和它本身以外不再有其他因数的自然数;合数是指自然数中除了能被 1 和本身整除外,还能被其他数(0 除外)整除的数。
答案:
质数:2,3,17;
合数:6,9,20,18。
答案:
质数:2,3,17;
合数:6,9,20,18。
例 3 把 45 分解质因数。
【解析】方法一:“树枝”图式分解法。
或

$ 45 = 5 × 3 × 3 $ $ 45 = 3 × 3 × 5 $
两种分解实质上是相同的。
方法二:短除法分解质因数。
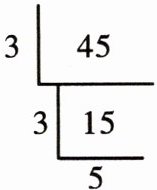
【答案】$ 45 = 3 × 3 × 5 $
【解析】方法一:“树枝”图式分解法。
或

$ 45 = 5 × 3 × 3 $ $ 45 = 3 × 3 × 5 $
两种分解实质上是相同的。
方法二:短除法分解质因数。

【答案】$ 45 = 3 × 3 × 5 $
答案:
解析:本题考查分解质因数的方法,包括“树枝”图式分解法和短除法。
“树枝”图式分解法是从一个数出发,不断找出能整除它的质数,直到分解为多个质数的乘积。
短除法是用质数依次去除这个数,将每次的除数和商继续相除,直到商为质数,最后把所有除数和最后的商相乘得到原数。
答案:$45 = 3×3×5$。
“树枝”图式分解法是从一个数出发,不断找出能整除它的质数,直到分解为多个质数的乘积。
短除法是用质数依次去除这个数,将每次的除数和商继续相除,直到商为质数,最后把所有除数和最后的商相乘得到原数。
答案:$45 = 3×3×5$。
例 4 把 35 个苹果和 46 个梨分给若干个小朋友,每个小朋友分得梨的个数相同,苹果的个数也相同,结果梨剩下 1 个,苹果正好分完,则小朋友最多有几个?
【解析】每个小朋友得到的苹果一样多,梨也一样多,小朋友的人数是所分梨的个数和苹果的个数的公因数。因为剩下 1 个梨,所以所分梨的个数应是 $ 46 - 1 = 45 $(个),即所求的小朋友最多有几个就是求 35 和 45 的最大公因数。
【答案】$ 46 - 1 = 45 $(个)
45 的因数:1,3,5,9,15,45;
35 的因数:1,5,7,35;
45 和 35 的公因数:1,5;
45 和 35 的最大公因数是 5。
答:小朋友最多有 5 个。
【解析】每个小朋友得到的苹果一样多,梨也一样多,小朋友的人数是所分梨的个数和苹果的个数的公因数。因为剩下 1 个梨,所以所分梨的个数应是 $ 46 - 1 = 45 $(个),即所求的小朋友最多有几个就是求 35 和 45 的最大公因数。
【答案】$ 46 - 1 = 45 $(个)
45 的因数:1,3,5,9,15,45;
35 的因数:1,5,7,35;
45 和 35 的公因数:1,5;
45 和 35 的最大公因数是 5。
答:小朋友最多有 5 个。
答案:
【解析】题目考查的是因数与倍数中最大公因数的应用。
需要找到35和45的最大公因数,这个最大公因数就是小朋友的最多人数。
首先,根据题目条件,梨剩下1个,所以实际分出去的梨是46-1=45(个)。
然后求35和45的最大公因数。
分别列出35和45的因数:
35的因数:1,5,7,35。
45的因数:1,3,5,9,15,45。
接着找出它们的公因数:1,5。
其中最大的公因数是5。
【答案】46 - 1 = 45(个)。
45的因数:1,3,5,9,15,45;
35的因数:1,5,7,35;
45和35的最大公因数是5。
所以小朋友最多有 5 个。
需要找到35和45的最大公因数,这个最大公因数就是小朋友的最多人数。
首先,根据题目条件,梨剩下1个,所以实际分出去的梨是46-1=45(个)。
然后求35和45的最大公因数。
分别列出35和45的因数:
35的因数:1,5,7,35。
45的因数:1,3,5,9,15,45。
接着找出它们的公因数:1,5。
其中最大的公因数是5。
【答案】46 - 1 = 45(个)。
45的因数:1,3,5,9,15,45;
35的因数:1,5,7,35;
45和35的最大公因数是5。
所以小朋友最多有 5 个。
例 5 有一箱面包,不论是平均分给 8 个人,还是平均分给 6 个人,都多 2 块,这箱面包至少有多少块?
【解析】由已知条件可知,这箱面包的块数减去 2 后,正好是 8 和 6 的公倍数,也就是说,这箱面包的块数比 8 和 6 的公倍数多 2,求至少有多少块,就是求 8 和 6 的最小公倍数再加上 2 的值。
【答案】8 的倍数:8,16,24,32,40……;6 的倍数:6,12,18,24……;8 和 6 的最小公倍数是 24。
$ 24 + 2 = 26 $(块)
答:这箱面包至少有 26 块。
【解析】由已知条件可知,这箱面包的块数减去 2 后,正好是 8 和 6 的公倍数,也就是说,这箱面包的块数比 8 和 6 的公倍数多 2,求至少有多少块,就是求 8 和 6 的最小公倍数再加上 2 的值。
【答案】8 的倍数:8,16,24,32,40……;6 的倍数:6,12,18,24……;8 和 6 的最小公倍数是 24。
$ 24 + 2 = 26 $(块)
答:这箱面包至少有 26 块。
答案:
【解析】
题目考查最小公倍数的应用。由题可知,这箱面包的块数减去2后,必须是8和6的公倍数。要求这箱面包至少有多少块,需要先找到8和6的最小公倍数,然后再加上2。
首先,我们找到8和6的最小公倍数:
8的质因数分解为$2 × 2 × 2$,
6的质因数分解为$2 × 3$,
所以,8和6的最小公倍数为$2 × 2 × 2 × 3 = 24$,
然后,将这个最小公倍数加上2,即可得到这箱面包至少有多少块:
$24 + 2 = 26$(块),
所以,这箱面包至少有26块。
【答案】
8的倍数有:8,16,24,32,40……;
6的倍数有:6,12,18,24……;
8和6的最小公倍数是24;
$24 + 2 = 26$(块);
答:这箱面包至少有26块。
题目考查最小公倍数的应用。由题可知,这箱面包的块数减去2后,必须是8和6的公倍数。要求这箱面包至少有多少块,需要先找到8和6的最小公倍数,然后再加上2。
首先,我们找到8和6的最小公倍数:
8的质因数分解为$2 × 2 × 2$,
6的质因数分解为$2 × 3$,
所以,8和6的最小公倍数为$2 × 2 × 2 × 3 = 24$,
然后,将这个最小公倍数加上2,即可得到这箱面包至少有多少块:
$24 + 2 = 26$(块),
所以,这箱面包至少有26块。
【答案】
8的倍数有:8,16,24,32,40……;
6的倍数有:6,12,18,24……;
8和6的最小公倍数是24;
$24 + 2 = 26$(块);
答:这箱面包至少有26块。
查看更多完整答案,请扫码查看


