2025年暑假集训合肥工业大学出版社五年级数学苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假集训合肥工业大学出版社五年级数学苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
例1 根据等式的性质在 $ ◯ $ 里填运算符号,在 $ □ $ 里填数。
$ x + 32 = 48 $
解:$ x + 32 $
$ x = $
$ x + 32 = 48 $
解:$ x + 32 $
-
32
$ = 48 $-
32
$ x = $
16
答案:
【解析】本题考查根据等式的性质解方程。等式的性质(一)表明,等式两边同时加上或减去同一个数,等式仍然成立。在方程$x + 32 = 48$中,为了得到$x$的值,需要在等式两边同时减去$32$。
【答案】解:$x + 32 - 32 = 48 - 32$
$x = 16$
【答案】解:$x + 32 - 32 = 48 - 32$
$x = 16$
例2 看图列方程并解答。
平行四边形的面积是270平方分米
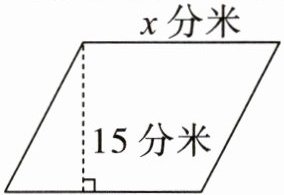
【解析】观察题图,本题已知平行四边形的面积和高,求平行四边形对应的底。我们可以根据“底 $ × $ 高 $ = $ 平行四边形的面积”列出方程,再根据等式的性质(二)来解方程。在求出未知数 $ x $ 的值后,要自觉进行检验。
【答案】解:$ 15x = 270 $
$ 15x ÷ 15 = 270 ÷ 15 $
$ x = 18 $
答:平行四边形的底边长为 18 分米。
平行四边形的面积是270平方分米

【解析】观察题图,本题已知平行四边形的面积和高,求平行四边形对应的底。我们可以根据“底 $ × $ 高 $ = $ 平行四边形的面积”列出方程,再根据等式的性质(二)来解方程。在求出未知数 $ x $ 的值后,要自觉进行检验。
【答案】解:$ 15x = 270 $
$ 15x ÷ 15 = 270 ÷ 15 $
$ x = 18 $
答:平行四边形的底边长为 18 分米。
答案:
【解析】本题可根据平行四边形的面积公式列出方程,再利用等式的性质求解方程,最后进行检验。
平行四边形的面积公式为$底×高$,已知面积是$270$平方分米,高是$15$分米,底是$x$分米,所以可列出方程$15x = 270$,再根据等式的性质,等式两边同时除以$15$来求解$x$。
【答案】
解:$15x = 270$
$15x÷15 = 270÷15$
$x = 18$
答:平行四边形的底边长为$18$分米。
平行四边形的面积公式为$底×高$,已知面积是$270$平方分米,高是$15$分米,底是$x$分米,所以可列出方程$15x = 270$,再根据等式的性质,等式两边同时除以$15$来求解$x$。
【答案】
解:$15x = 270$
$15x÷15 = 270÷15$
$x = 18$
答:平行四边形的底边长为$18$分米。
知识点3 用形如“$ ax \pm b = c (a \neq 0) $”的方程解决实际问题
例3 我国第二个目标飞行器“天宫二号”,全长 10.4 米,比它最大直径的 4 倍少 3 米,“天宫二号”的最大直径是多少米?
【解析】根据关键句“‘天宫二号’的长度比它最大直径的 4 倍少 3 米”,想到等量关系式: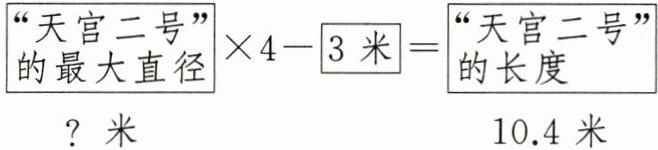
其中,“天宫二号”的最大直径未知,可以设为 $ x $,列方程解答。
【答案】解:设“天宫二号”的最大直径是 $ x $ 米。
$ 4x - 3 = 10.4 $
$ 4x - 3 + 3 = 10.4 + 3 $
$ 4x = 13.4 $
$ x = 3.35 $
答:“天宫二号”的最大直径是 3.35 米。
例3 我国第二个目标飞行器“天宫二号”,全长 10.4 米,比它最大直径的 4 倍少 3 米,“天宫二号”的最大直径是多少米?
【解析】根据关键句“‘天宫二号’的长度比它最大直径的 4 倍少 3 米”,想到等量关系式:

其中,“天宫二号”的最大直径未知,可以设为 $ x $,列方程解答。
【答案】解:设“天宫二号”的最大直径是 $ x $ 米。
$ 4x - 3 = 10.4 $
$ 4x - 3 + 3 = 10.4 + 3 $
$ 4x = 13.4 $
$ x = 3.35 $
答:“天宫二号”的最大直径是 3.35 米。
答案:
解析:本题考查的是通过设未知数,根据题目中的数量关系列方程来求解实际问题。关键在于找出“天宫二号”长度与最大直径之间的等量关系,即最大直径的$4$倍少$3$米等于“天宫二号”的全长。
答案:解:设“天宫二号”的最大直径是$x$米。
$4x - 3 = 10.4$
$4x - 3 + 3 = 10.4 + 3$
$4x = 13.4$
$x = 3.35$
答:“天宫二号”的最大直径是$3.35$米。
答案:解:设“天宫二号”的最大直径是$x$米。
$4x - 3 = 10.4$
$4x - 3 + 3 = 10.4 + 3$
$4x = 13.4$
$x = 3.35$
答:“天宫二号”的最大直径是$3.35$米。
知识点4 用形如“$ ax \pm bx = c (a \neq 0, b \neq 0) $”的方程解决实际问题
例4 富民果园种植的桃树比梨树多 1200 棵,其中桃树的棵数是梨树的 3 倍,富民果园种植桃树和梨树各多少棵?
【解析】题目中有两个表示数量之间关系的条件,由“桃树的棵数是梨树的 3 倍”,我们可以设梨树有 $ x $ 棵,桃树有 $ 3x $ 棵。由“种植的桃树比梨树多 1200 棵”,我们可以想到:
用线段图表示出来就是:
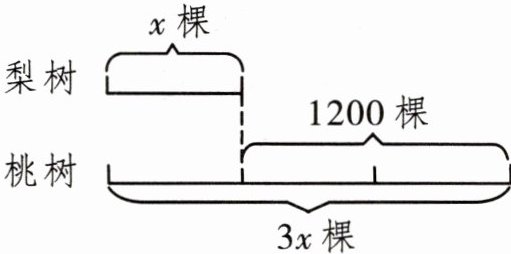
根据两个数量之间“差”的关系列出方程并解答。
【答案】解:设梨树有 $ x $ 棵,桃树有 $ 3x $ 棵。
$ 3x - x = 1200 $
$ 2x = 1200 $
$ x = 600 $
$ 3x = 3 × 600 = 1800 $
答:梨树有 600 棵,桃树有 1800 棵。
例4 富民果园种植的桃树比梨树多 1200 棵,其中桃树的棵数是梨树的 3 倍,富民果园种植桃树和梨树各多少棵?
【解析】题目中有两个表示数量之间关系的条件,由“桃树的棵数是梨树的 3 倍”,我们可以设梨树有 $ x $ 棵,桃树有 $ 3x $ 棵。由“种植的桃树比梨树多 1200 棵”,我们可以想到:

用线段图表示出来就是:

根据两个数量之间“差”的关系列出方程并解答。
【答案】解:设梨树有 $ x $ 棵,桃树有 $ 3x $ 棵。
$ 3x - x = 1200 $
$ 2x = 1200 $
$ x = 600 $
$ 3x = 3 × 600 = 1800 $
答:梨树有 600 棵,桃树有 1800 棵。
答案:
解:设梨树有 $ x $ 棵,桃树有 $ 3x $ 棵。
$ 3x - x = 1200 $
$ 2x = 1200 $
$ x = 600 $
$ 3x = 3×600 = 1800 $
答:梨树有 600 棵,桃树有 1800 棵。
$ 3x - x = 1200 $
$ 2x = 1200 $
$ x = 600 $
$ 3x = 3×600 = 1800 $
答:梨树有 600 棵,桃树有 1800 棵。
查看更多完整答案,请扫码查看


