《2025年轻松作业本八年级数学上册苏科版》

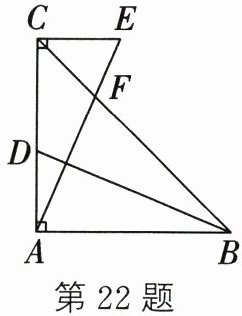
22. 如图,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = AC$,$EC\perp AC$,垂足为$C$,$AE交线段BC于F$,$D是AC$边上一点,连接$BD$,且$BD = AE$.
(1) 求证:$CE = AD$;
(2) $BD与AE$有怎样的位置关系? 证明你的结论;
(3) 当$\angle CFE = \angle ADB$时,求证:$BD平分\angle ABC$.

答案：
（1）证明：$\because \angle BAC = 90^{\circ}$，$EC \perp AC$，$\therefore \angle ACE = \angle BAD = 90^{\circ}$。在$\mathrm{Rt} \triangle ACE$和$\mathrm{Rt} \triangle BAD$中，$\begin{cases} AE = BD \\ CA = AB \end{cases}$，$\therefore \mathrm{Rt} \triangle ACE \cong \mathrm{Rt} \triangle BAD (\mathrm{HL})$。$\therefore CE = AD$；（2）$BD \perp AE$，证明：如图，$\because \triangle ACE \cong \triangle BAD$，$\therefore \angle CAE = \angle ABD$。$\therefore \angle AOD = \angle BAE + \angle ABD = \angle BAE + \angle CAE = \angle BAC = 90^{\circ}$。$\therefore AE \perp BD$；（3）证明：$\because \angle ADB + \angle DAE = \angle DAE + \angle BAE = 90^{\circ}$，$\therefore \angle ADB = \angle BAE$。$\because \angle CFE = \angle ADB$，$\angle CFE = \angle AFB$，$\therefore \angle AFB = \angle BAE$。$\therefore FB = AB$。$\because BD \perp AE$，$\therefore \angle ABD = \angle FBD$，即$BD$平分$\angle ABC$。

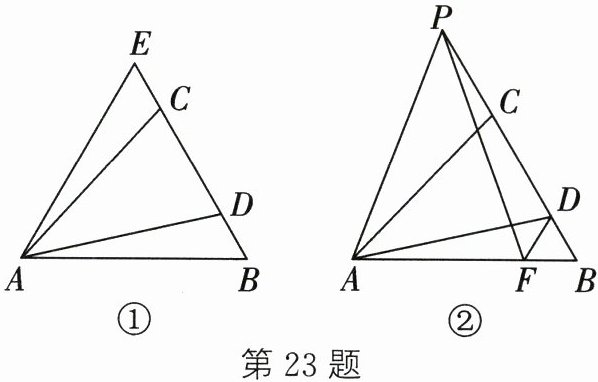
23. 在$\triangle ABC$中,$\angle B = 60^{\circ}$,$D是BC$上的一点,且$AD = AC$.
(1) 如图①,延长$BC到E$,使$CE = BD$,连接$AE$.求证:$AB = AE$;
(2) 如图②,在$AB上取一点F$,使$DF = DB$,$P为BC$延长线上的一点,连接$PA$、$PF$,若$PA = PF$,猜想$PC与BD$的数量关系并证明.

答案：
（1）证明：在$\triangle ACD$中，$AD = AC$，$\therefore \angle ADC = \angle ACD$。$\therefore \angle ADB = \angle ACE$。在$\triangle ADB$和$\triangle ACE$中，$\begin{cases} AD = AC \\ \angle ADB = \angle ACE \\ BD = CE \end{cases}$，$\therefore \triangle ADB \cong \triangle ACE (\mathrm{SAS})$。$\therefore AB = AE$；（2）解：$PC$与$BD$的数量关系为：$PC = 2BD$，理由如下：在线段$PC$上取一点$E$，使$CE = BD$，连接$AE$，如图所示：由（1）得：$\triangle ADB \cong \triangle ACE (\mathrm{SAS})$，$\therefore \angle AEC = \angle B = 60^{\circ}$。$\therefore \angle AEP = 120^{\circ}$。$\because DF = DB$，$\angle B = 60^{\circ}$，$\therefore \triangle DBF$是等边三角形。$\therefore \angle FDB = \angle DFB = 60^{\circ}$。$\therefore \angle PFD + \angle PFA = 120^{\circ}$，$\angle PDF = 120^{\circ}$。$\therefore \angle AEP = \angle PDF$。$\because PA = PF$，$\therefore \angle PAF = \angle PFA$。$\because \angle APE + \angle PAF = 120^{\circ}$，$\therefore \angle APE = \angle PFD$。在$\triangle APE$和$\triangle PFD$中，$\begin{cases} \angle AEP = \angle PDF \\ \angle APE = \angle PFD \\ PA = PF \end{cases}$，$\therefore \triangle APE \cong \triangle PFD$。$\therefore PE = DF = BD = CE$。$\therefore PC = 2BD$。

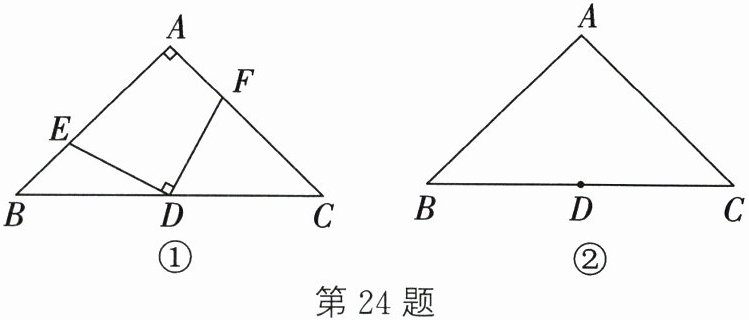
24. 在$\triangle ABC$中,$\angle A = 90^{\circ}$,$AB = AC$,点$D为BC$的中点.
(1) 如图①,若点$E$、$F分别为AB$、$AC$上的点,且$DE\perp DF$,求证:$BE = AF$;
(2) 若点$E$、$F分别为AB$、$CA$延长线上的点,且$DE\perp DF$,那么$BE = AF$吗? 请利用图②说明理由.

答案：
（1）证明：连接$AD$，如图①所示。$\because \angle A = 90^{\circ}$，$AB = AC$，$\therefore \triangle ABC$为等腰直角三角形，$\angle EBD = 45^{\circ}$。$\because$点$D$为$BC$的中点，$\therefore AD = \frac{1}{2}BC = BD$，$\angle FAD = 45^{\circ}$。$\because \angle BDE + \angle EDA = 90^{\circ}$，$\angle EDA + \angle ADF = 90^{\circ}$，$\therefore \angle BDE = \angle ADF$。在$\triangle BDE$和$\triangle ADF$中，$\begin{cases} \angle EBD = \angle FAD \\ BD = AD \\ \angle BDE = \angle ADF \end{cases}$，$\therefore \triangle BDE \cong \triangle ADF (\mathrm{ASA})$。$\therefore BE = AF$；（2）$BE = AF$，理由：连接$AD$，如图②所示。$\because \angle ABD = \angle BAD = 45^{\circ}$，$\therefore \angle EBD = \angle FAD = 135^{\circ}$。$\because \angle EDB + \angle BDF = 90^{\circ}$，$\angle BDF + \angle FDA = 90^{\circ}$，$\therefore \angle EDB = \angle FDA$。在$\triangle EDB$和$\triangle FDA$中，$\begin{cases} \angle EBD = \angle FAD \\ BD = AD \\ \angle EBD = \angle FDA \end{cases}$，$\therefore \triangle EDB \cong \triangle FDA (\mathrm{ASA})$。$\therefore BE = AF$。