1. 在$\triangle ABC$中,$∠A$、$∠B$、$∠C的对边分别为a$、$b$、$c$,下列条件中,不能判断$\triangle ABC$为直角三角形的是 (
A. $∠A:∠B:∠C= 3:4:5$
B. $a^{2}= 1$,$b^{2}= 2$,$c^{2}= 3$
C. $(b+c)(b-c)= a^{2}$
D. $∠A-∠B= ∠C$
A
)A. $∠A:∠B:∠C= 3:4:5$
B. $a^{2}= 1$,$b^{2}= 2$,$c^{2}= 3$
C. $(b+c)(b-c)= a^{2}$
D. $∠A-∠B= ∠C$
答案:
A
2. 下列给出的四组数中,能构成直角三角形三边的一组是 (
A. 1,2,3
B. 2,3,4
C. 5,12,13
D. 13,14,15
C
)A. 1,2,3
B. 2,3,4
C. 5,12,13
D. 13,14,15
答案:
C
3. 如图,长方形$ABCD$中,$AB= 3cm$,$AD= 9cm$,将此长方形折叠,使点$B与点D$重合,折痕为$EF$,则$\triangle ABE$的面积为 (
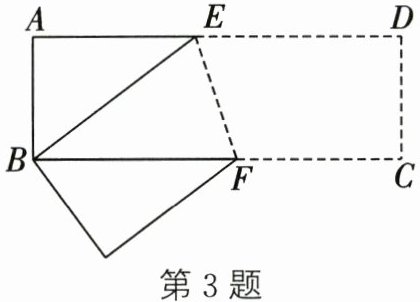
A. $3cm^{2}$
B. $4cm^{2}$
C. $6cm^{2}$
D. $12cm^{2}$
C
)
A. $3cm^{2}$
B. $4cm^{2}$
C. $6cm^{2}$
D. $12cm^{2}$
答案:
C
4. 在$\triangle ABC$中,$AB= 15$,$AC= 13$,高$AD= 12$,则$\triangle ABC$的周长为 (
A. 42
B. 32
C. 32或42
D. 33或37
C
)A. 42
B. 32
C. 32或42
D. 33或37
答案:
C
5. 若直角三角形的两边长分别为$a$、$b$,且满足$\sqrt{(a-3)^{2}}+|b-4|= 0$,则该直角三角形的第三边长为 (
A. 5
B. $\sqrt{7}$
C. 4
D. 5或$\sqrt{7}$
D
)A. 5
B. $\sqrt{7}$
C. 4
D. 5或$\sqrt{7}$
答案:
D
6. 小明学了在数轴上画出表示无理数的点的方法后,进行练习:首先画数轴,原点为$O$,在数轴上找到表示数2的点$A$,然后过点$A作AB\perp OA$,使$AB= 3$(如图).以$O$为圆心,$OB$长为半径作弧,交数轴正半轴于点$P$,则点$P$所表示的数介于 (
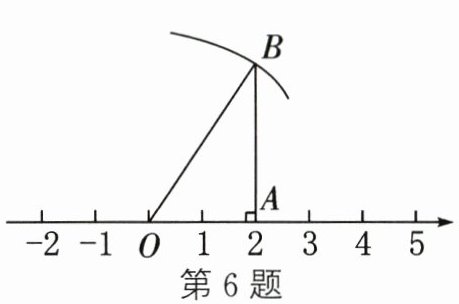
A. 1和2之间
B. 2和3之间
C. 3和4之间
D. 4和5之间
C
)
A. 1和2之间
B. 2和3之间
C. 3和4之间
D. 4和5之间
答案:
C
7. 我国古代数学著作《九章算术》中有这样一个问题:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深几何(注:丈、尺是长度单位,1丈= 10尺)? 意思为:如图,有一个边长为1丈的正方形水池,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的岸边,它的顶端恰好碰到池边的水面.则这根芦苇的长度是 (
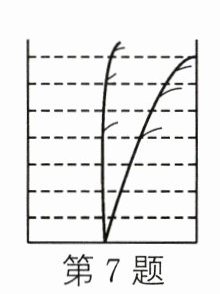
A. 5尺
B. 10尺
C. 12尺
D. 13尺
D
)
A. 5尺
B. 10尺
C. 12尺
D. 13尺
答案:
D
8. 如图,高速公路上$A$、$B$两点相距10km,$C$、$D$为两村庄,已知$DA= 4km$,$CB= 6km$,$DA\perp AB于A$,$CB\perp AB于B$.现要在$AB上建一个服务站E$,使得$C$、$D两村庄到E$站的距离相等,则$EA$的长是 (
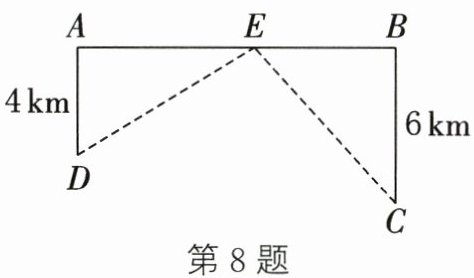
A. 4km
B. 5km
C. 6km
D. 7km
C
)
A. 4km
B. 5km
C. 6km
D. 7km
答案:
C
查看更多完整答案,请扫码查看


