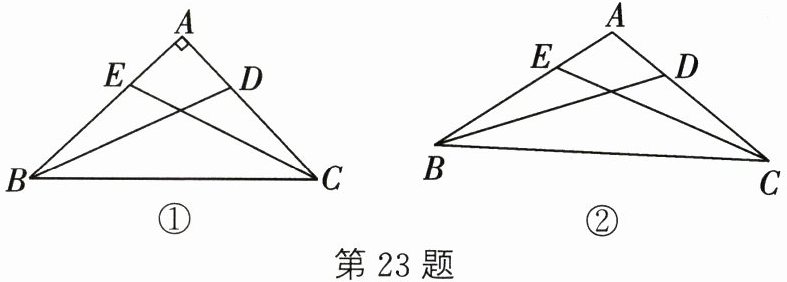
23.在$\triangle ABC$中,$AB = AC$,点D、E分别在AC、AB上,且$BD = CE$。
(1)如图①,$\angle BAC = 90^{\circ}$,求证:$AE = AD$;
(2)如图②,当$90^{\circ}<\angle BAC<180^{\circ}$时,(1)中结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由。
(1)如图①,$\angle BAC = 90^{\circ}$,求证:$AE = AD$;
(2)如图②,当$90^{\circ}<\angle BAC<180^{\circ}$时,(1)中结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由。

答案:
(1)证明:在$Rt\triangle ABD$和$Rt\triangle ACE$中,$\begin{cases}AB = AC\\BD = CE\end{cases}$,$\therefore Rt\triangle ABD \cong Rt\triangle ACE(HL)$,$\therefore AD = AE$;(2)解:(1)中结论仍然成立。证明:过点$B$作$BF \perp AC$于点$F$,过点$C$作$CG \perp BA$于点$G$。$\because \begin{cases}\angle BAF = \angle CAG\\\angle F = \angle G\\AB = AC\end{cases}$,$\therefore \triangle ABF \cong \triangle ACG$,$\therefore AF = AG$,$BF = CG$。在$Rt\triangle DBF$和$Rt\triangle ECG$中,$\begin{cases}BD = CE\\BF = CG\end{cases}$,$\therefore Rt\triangle DBF \cong Rt\triangle ECG(HL)$,$\therefore DF = EG$,$\therefore DF - AF = EG - AG$,$\therefore AD = AE$。
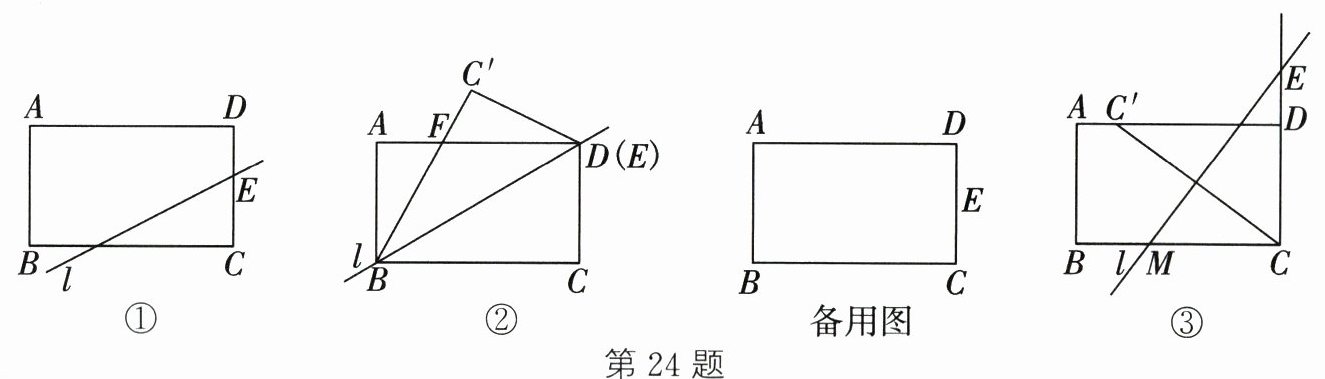
24.如图①,在四边形ABCD中,$\angle A= \angle B= \angle C= \angle D = 90^{\circ}$,$AB = CD = 6$,$BC = AD = 10$,点E是射线CD上一动点,点C沿过点E的直线l翻折得到点$C'$。
(1)直线l过点B。
① 如图②,若点E运动到点D,连接$BC'$交AD于点F,求DF长;
② 连接$CC'和C'D$,当点E在射线CD上移动时,是否存在某个位置,使得$\triangle CC'D$是直角三角形?若存在,请直接写出线段CE的长;若不存在,请说明理由;
(2)如图③,若点$C'$落在边AD上,直线l与折线$AB - BC$的交点为M,当点$C'$从点D移动到点A的过程中,点M的移动路径长为______。
(1)直线l过点B。
① 如图②,若点E运动到点D,连接$BC'$交AD于点F,求DF长;
② 连接$CC'和C'D$,当点E在射线CD上移动时,是否存在某个位置,使得$\triangle CC'D$是直角三角形?若存在,请直接写出线段CE的长;若不存在,请说明理由;
(2)如图③,若点$C'$落在边AD上,直线l与折线$AB - BC$的交点为M,当点$C'$从点D移动到点A的过程中,点M的移动路径长为______。

答案:
解:(1)①$\because \angle A = \angle ABC = 90^{\circ}$,$\therefore \angle A + \angle ABC = 180^{\circ}$,$\therefore AD // BC$,$\therefore \angle ADB = \angle CBD$。由翻折得$\angle C'B D = \angle CBD$,$\therefore \angle C'B D = \angle ADB$,$\therefore DF = BF$。$\because AB = CD = 6$,$BC = AD = 10$,$\therefore AF = 10 - DF$。$\because AF^{2} + AB^{2} = BF^{2}$,$\therefore (10 - DF)^{2} + 6^{2} = DF^{2}$,解得$DF = \frac{34}{5}$,$\therefore DF$的长是$\frac{34}{5}$。②如图①,$\angle CC'D = 90^{\circ}$,连接$EC'$。$\because$点$C'$与点$C$关于直线$l$对称,$\therefore BE$垂直平分$CC'$,$\therefore C'E = CE$,$\therefore \angle EC'C = \angle ECC'$。$\because \angle EC'D + \angle EC'C = 90^{\circ}$,$\angle EDC' + \angle ECC' = 90^{\circ}$,$\therefore \angle EC'D = \angle EDC'$,$\therefore C'E = DE$,$\therefore CE = DE = \frac{1}{2}CD = 3$;如图②,$\angle CDC' = 90^{\circ}$,点$E$在$CD$上。$\because \angle CDC' = \angle CDA = 90^{\circ}$,$\therefore$点$C'$在$AD$上,连接$EC'$、$BC'$。$\because BE$垂直平分$CC'$,$\therefore BC' = BC = 10$,$C'E = CE$,$\therefore AC' = \sqrt{BC'^{2} - AB^{2}} = \sqrt{10^{2} - 6^{2}} = 8$,$\therefore C'D = AD - AC' = 10 - 8 = 2$。$\because C'D^{2} + DE^{2} = C'E^{2}$,$DE = 6 - CE$,$\therefore 2^{2} + (6 - CE)^{2} = CE^{2}$,解得$CE = \frac{10}{3}$;如图③,$\angle CDC' = 90^{\circ}$,点$E$在$CD$的延长线上。$\because \angle CDC' = \angle CDA = 90^{\circ}$,$\therefore$点$C'$在$AD$的延长线上,连接$EC'$、$BC'$。$\because BE$垂直平分$CC'$,$\therefore BC' = BC = 10$,$C'E = CE$,$\therefore AC' = \sqrt{BC'^{2} - AB^{2}} = \sqrt{10^{2} - 6^{2}} = 8$,$\therefore C'D = AD + AC' = 10 + 8 = 18$。$\because \angle CDE' = 90^{\circ}$,$DE = CE - 6$,$\therefore C'D^{2} + DE^{2} = C'E^{2}$,$\therefore 18^{2} + (CE - 6)^{2} = CE^{2}$,解得$CE = 30$。综上所述,$CE$的长为$3$或$\frac{10}{3}$或$30$。(2)如图④,点$C'$与点$D$重合。$\because ME$垂直平分$CC'$,$\therefore ME$垂直平分$CD$,$\therefore \angle CEM = 90^{\circ}$,$\therefore \angle CEM + \angle C = 180^{\circ}$,$\therefore EM // BC$。$\because CE \perp BC$,$BM \perp BC$,$\therefore BM = CE = DE = \frac{1}{2}CD = 3$;如图⑤,连接$C'M$、$CC'$,$C'M \perp BC$。$\because AD // BC$,$AB \perp BC$,$\therefore C'M = AB = 6$。$\because ME$垂直平分$CC'$,$\therefore CM = C'M = 6$,$\therefore BM = BC - CM = 10 - 6 = 4$,$\therefore 3 + 4 = 7$,当点$C'$从图④的位置移动到图⑤的位置时,点$M$移动的距离为$7$;如图⑥,点$C'$与点$A$重合,连接$AM$、$AC$。$\because ME$垂直平分$CC'$,$\therefore ME$垂直平分$CA$,$\therefore AM = CM = 10 - BM$。$\because AB^{2} + BM^{2} = AM^{2}$,$\therefore 6^{2} + BM^{2} = (10 - BM)^{2}$,解得$BM = \frac{16}{5}$。$\therefore 4 - \frac{16}{5} = \frac{4}{5}$,当点$C'$从图⑤的位置移动到图⑥的位置时,点$M$移动的距离为$\frac{4}{5}$。$\therefore 7 + \frac{4}{5} = \frac{39}{5}$,$\therefore$当点$C'$从点$D$移动到点$A$的过程中,点$M$的移动路径长为$\frac{39}{5}$。

解:(1)①$\because \angle A = \angle ABC = 90^{\circ}$,$\therefore \angle A + \angle ABC = 180^{\circ}$,$\therefore AD // BC$,$\therefore \angle ADB = \angle CBD$。由翻折得$\angle C'B D = \angle CBD$,$\therefore \angle C'B D = \angle ADB$,$\therefore DF = BF$。$\because AB = CD = 6$,$BC = AD = 10$,$\therefore AF = 10 - DF$。$\because AF^{2} + AB^{2} = BF^{2}$,$\therefore (10 - DF)^{2} + 6^{2} = DF^{2}$,解得$DF = \frac{34}{5}$,$\therefore DF$的长是$\frac{34}{5}$。②如图①,$\angle CC'D = 90^{\circ}$,连接$EC'$。$\because$点$C'$与点$C$关于直线$l$对称,$\therefore BE$垂直平分$CC'$,$\therefore C'E = CE$,$\therefore \angle EC'C = \angle ECC'$。$\because \angle EC'D + \angle EC'C = 90^{\circ}$,$\angle EDC' + \angle ECC' = 90^{\circ}$,$\therefore \angle EC'D = \angle EDC'$,$\therefore C'E = DE$,$\therefore CE = DE = \frac{1}{2}CD = 3$;如图②,$\angle CDC' = 90^{\circ}$,点$E$在$CD$上。$\because \angle CDC' = \angle CDA = 90^{\circ}$,$\therefore$点$C'$在$AD$上,连接$EC'$、$BC'$。$\because BE$垂直平分$CC'$,$\therefore BC' = BC = 10$,$C'E = CE$,$\therefore AC' = \sqrt{BC'^{2} - AB^{2}} = \sqrt{10^{2} - 6^{2}} = 8$,$\therefore C'D = AD - AC' = 10 - 8 = 2$。$\because C'D^{2} + DE^{2} = C'E^{2}$,$DE = 6 - CE$,$\therefore 2^{2} + (6 - CE)^{2} = CE^{2}$,解得$CE = \frac{10}{3}$;如图③,$\angle CDC' = 90^{\circ}$,点$E$在$CD$的延长线上。$\because \angle CDC' = \angle CDA = 90^{\circ}$,$\therefore$点$C'$在$AD$的延长线上,连接$EC'$、$BC'$。$\because BE$垂直平分$CC'$,$\therefore BC' = BC = 10$,$C'E = CE$,$\therefore AC' = \sqrt{BC'^{2} - AB^{2}} = \sqrt{10^{2} - 6^{2}} = 8$,$\therefore C'D = AD + AC' = 10 + 8 = 18$。$\because \angle CDE' = 90^{\circ}$,$DE = CE - 6$,$\therefore C'D^{2} + DE^{2} = C'E^{2}$,$\therefore 18^{2} + (CE - 6)^{2} = CE^{2}$,解得$CE = 30$。综上所述,$CE$的长为$3$或$\frac{10}{3}$或$30$。(2)如图④,点$C'$与点$D$重合。$\because ME$垂直平分$CC'$,$\therefore ME$垂直平分$CD$,$\therefore \angle CEM = 90^{\circ}$,$\therefore \angle CEM + \angle C = 180^{\circ}$,$\therefore EM // BC$。$\because CE \perp BC$,$BM \perp BC$,$\therefore BM = CE = DE = \frac{1}{2}CD = 3$;如图⑤,连接$C'M$、$CC'$,$C'M \perp BC$。$\because AD // BC$,$AB \perp BC$,$\therefore C'M = AB = 6$。$\because ME$垂直平分$CC'$,$\therefore CM = C'M = 6$,$\therefore BM = BC - CM = 10 - 6 = 4$,$\therefore 3 + 4 = 7$,当点$C'$从图④的位置移动到图⑤的位置时,点$M$移动的距离为$7$;如图⑥,点$C'$与点$A$重合,连接$AM$、$AC$。$\because ME$垂直平分$CC'$,$\therefore ME$垂直平分$CA$,$\therefore AM = CM = 10 - BM$。$\because AB^{2} + BM^{2} = AM^{2}$,$\therefore 6^{2} + BM^{2} = (10 - BM)^{2}$,解得$BM = \frac{16}{5}$。$\therefore 4 - \frac{16}{5} = \frac{4}{5}$,当点$C'$从图⑤的位置移动到图⑥的位置时,点$M$移动的距离为$\frac{4}{5}$。$\therefore 7 + \frac{4}{5} = \frac{39}{5}$,$\therefore$当点$C'$从点$D$移动到点$A$的过程中,点$M$的移动路径长为$\frac{39}{5}$。

查看更多完整答案,请扫码查看


