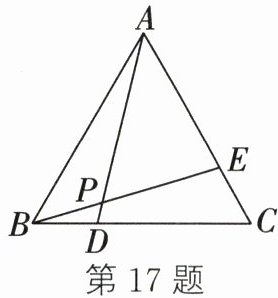
17. 如图,在等边三角形$ABC$中,$BD = CE$,$AD与BE相交于点P$,则$\angle APE$的度数是______
60
$^{\circ}$.
答案:
60
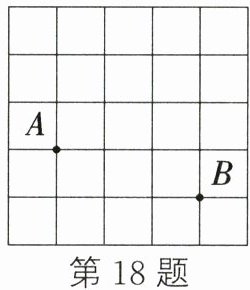
18. 如图,已知每个小方格的边长为1,$A$、$B$两点都在小方格的格点(顶点)上,请在图中找一个格点$C$,使$\triangle ABC$是等腰三角形,这样的格点$C$有
8
个.
答案:
8
19. 如图,利用尺规求作所有点$P$,使点$P$同时满足下列两个条件:① 点$P到A$、$B$两点的距离相等;② 点$P到直线l_1$、$l_2$的距离相等(要求保留作图痕迹,不必写出作法).
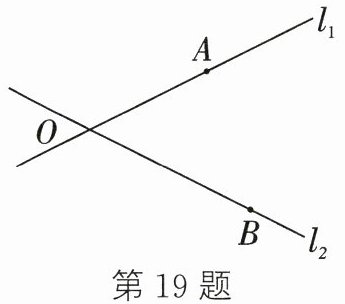

答案:
如图,点$P_{1}$、$P_{2}$即为所求作的点。

如图,点$P_{1}$、$P_{2}$即为所求作的点。

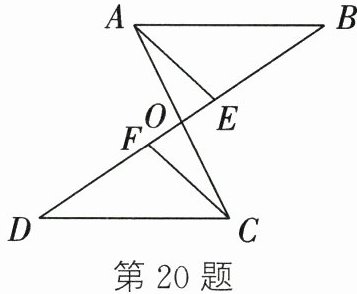
20. 如图,$AC$、$BD相交于点O$,$AB// CD$,$BF = DE$,$\angle OAE = \angle OCF$.求证:$AE = CF$.

答案:
证明:$\because AB // CD$,$\therefore \angle B = \angle D$,$\angle BAO = \angle DCO$。$\because \angle OAE = \angle OCF$,$\therefore \angle BAO - \angle OAE = \angle DCO - \angle OCF$。$\therefore \angle BAE = \angle DCF$。$\because BF = DE$,$\therefore BF - EF = DE - EF$。$\therefore BE = DF$,在$\triangle ABE$和$\triangle CDF$中,$\begin{cases} \angle B = \angle D \\ \angle BAE = \angle DCF \\ BE = DF \end{cases}$,$\therefore \triangle ABE \cong \triangle CDF$。$\therefore AE = CF$。
21. 如图,已知$\triangle ABF\cong \triangle CDE$.
(1) 若$\angle B = 30^{\circ}$,$\angle DCF = 40^{\circ}$,求$\angle EFC$的度数;
(2) 若$BD = 10$,$EF = 2$,求$BF$的长.
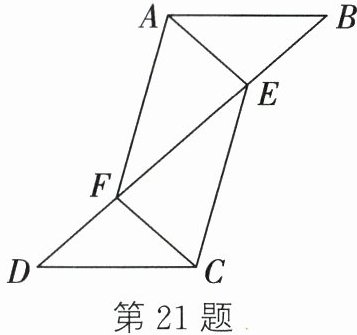
(1) 若$\angle B = 30^{\circ}$,$\angle DCF = 40^{\circ}$,求$\angle EFC$的度数;
(2) 若$BD = 10$,$EF = 2$,求$BF$的长.

答案:
解:(1)$\because \triangle ABF \cong \triangle CDE$,$\therefore \angle D = \angle B = 30^{\circ}$。$\therefore \angle EFC = \angle DCF + \angle D = 70^{\circ}$;(2)$\because \triangle ABF \cong \triangle CDE$,$\therefore BF = DE$。$\therefore BF - EF = DE - EF$,即$BE = DF$。$\because BD = 10$,$EF = 2$,$\therefore BE = (10 - 2) \div 2 = 4$。$\therefore BF = BE + EF = 6$。
查看更多完整答案,请扫码查看


