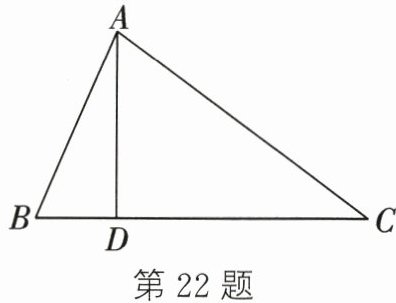
22. 如图,一棵大树$AD$两侧各有一条斜拉的绳子,大致如图所示,李明想用所学知识测量大树$AD$的高度,他从工作人员处了解到绳子$AB$的长为13m,$AC$的长为20m,然后用米尺测得$B$、$C$之间的距离为21m,已知$B$、$C$、$D$在一条直线上,$AD\perp BC$,求大树的高$AD$.

答案:
解:设$ BD = x m $,则$ CD = (21 - x) m $,$ \because AD ⊥ BC $,$ \therefore ∠ADB = ∠ADC = 90^{\circ} $。在$ Rt△ABD $中,$ AD^{2} = AB^{2} - BD^{2} $,在$ Rt△ACD $中,$ AD^{2} = AC^{2} - CD^{2} $。$ \therefore AB^{2} - BD^{2} = AC^{2} - CD^{2} $。$ \because AB = 13 m $,$ AC = 20 m $,$ \therefore 13^{2} - x^{2} = 20^{2} - (21 - x)^{2} $,解得$ x = 5 $,即$ BD = 5 m $。$ \therefore AD^{2} = AB^{2} - BD^{2} = 13^{2} - 5^{2} = 144 $,$ AD = 12(m) $。即大树的高AD为12m。
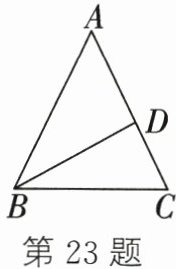
23. 如图,已知$\triangle ABC$中,$AB= AC$,$BC= 10$,$D是AC$上一点,且$CD= 6$,$BD= 8$.
(1) 求证:$\triangle BDC$是直角三角形;
(2) 求$AB$的长.
(1) 求证:$\triangle BDC$是直角三角形;
(2) 求$AB$的长.

答案:
(1) 证明:$ \because BC = 10 $,$ CD = 6 $,$ BD = 8 $,$ \therefore BC^{2} = 10^{2} = CD^{2} + BD^{2} = 6^{2} + 8^{2} $。$ \therefore ∠BDC = 90^{\circ} $。故$ △BDC $是直角三角形;
(2) 解:设$ AB = AC = x $,则$ AD = x - 6 $,$ \because ∠ADB = ∠BDC = 90^{\circ} $,$ \therefore AB^{2} = AD^{2} + BD^{2} $。$ \therefore x^{2} = (x - 6)^{2} + 8^{2} $,解得$ x = \frac{25}{3} $,故$ AB = \frac{25}{3} $。
(1) 证明:$ \because BC = 10 $,$ CD = 6 $,$ BD = 8 $,$ \therefore BC^{2} = 10^{2} = CD^{2} + BD^{2} = 6^{2} + 8^{2} $。$ \therefore ∠BDC = 90^{\circ} $。故$ △BDC $是直角三角形;
(2) 解:设$ AB = AC = x $,则$ AD = x - 6 $,$ \because ∠ADB = ∠BDC = 90^{\circ} $,$ \therefore AB^{2} = AD^{2} + BD^{2} $。$ \therefore x^{2} = (x - 6)^{2} + 8^{2} $,解得$ x = \frac{25}{3} $,故$ AB = \frac{25}{3} $。
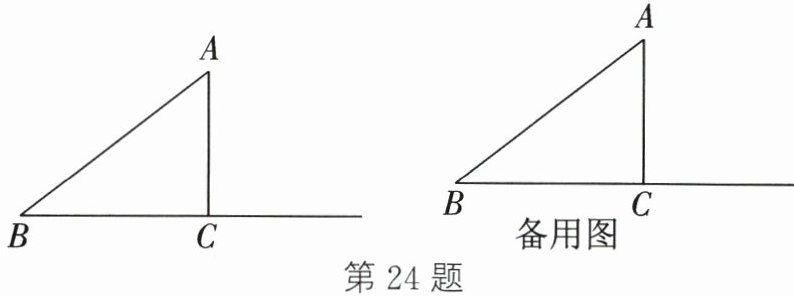
24. 如图,在$\triangle ABC$中,$∠ACB= 90^{\circ}$,$AB= 5cm$,$AC= 3cm$,动点$P从点B出发沿射线BC$以每秒1cm的速度运动,设运动的时间为$t$秒.
(1) 若$\triangle ABP是以BP$为斜边的直角三角形,求$t$的值;
(2) 若$\triangle ABP是以BP$为腰的等腰三角形,求$t$的值.
(1) 若$\triangle ABP是以BP$为斜边的直角三角形,求$t$的值;
(2) 若$\triangle ABP是以BP$为腰的等腰三角形,求$t$的值.

答案:
解:
(1) $ \because ∠ACB = 90^{\circ} $,$ AB = 5 cm $,$ AC = 3 cm $,$ \therefore BC = 4 $。$ \therefore CP = t - 4 $。由$ ∠ACP = ∠BAP = 90^{\circ} $,可得$ AP^{2} = t^{2} - 25 = (t - 4)^{2} + 9 $,解得$ t = \frac{25}{4} $;
(2) 当$ AB = BP $时,$ t = 5 $。当$ BP = AP $时,$ \therefore CP = 4 - t $,在$ Rt△APC $中,可得$ 9 + (4 - t)^{2} = t^{2} $,解得$ t = \frac{25}{8} $。综上所述,t的值为5或$ \frac{25}{8} $。
(1) $ \because ∠ACB = 90^{\circ} $,$ AB = 5 cm $,$ AC = 3 cm $,$ \therefore BC = 4 $。$ \therefore CP = t - 4 $。由$ ∠ACP = ∠BAP = 90^{\circ} $,可得$ AP^{2} = t^{2} - 25 = (t - 4)^{2} + 9 $,解得$ t = \frac{25}{4} $;
(2) 当$ AB = BP $时,$ t = 5 $。当$ BP = AP $时,$ \therefore CP = 4 - t $,在$ Rt△APC $中,可得$ 9 + (4 - t)^{2} = t^{2} $,解得$ t = \frac{25}{8} $。综上所述,t的值为5或$ \frac{25}{8} $。
查看更多完整答案,请扫码查看


