《2025年轻松作业本八年级数学上册苏科版》

19.已知下列9个数：① 0,② $-3\pi$,③ $\sqrt[3]{8}$,④ $\sqrt{100}$,⑤ $-\frac{22}{7}$,⑥ 2.$\dot{3}\dot{5}$,⑦ $-\sqrt{11}$,⑧ $\sqrt[3]{-5}$,⑨ 3.202002000⋯(两个2之间依次增加1个0)。请把这些数对应的编号,填入合适的集合中。
(1)有理数集合：\{①③④⑤⑥…\}；
(2)无理数集合：\{②⑦⑧⑨…\}；
(3)负实数集合：\{②⑤⑦⑧…\}。

答案： （1）①③④⑤⑥ （2）②⑦⑧⑨ （3）②⑤⑦⑧

20.如图,已知$\angle A= \angle D$,有下列五个条件：① $AE = DE$；② $BE = CE$；③ $AB = DC$；④ $\angle ABC= \angle DCB$；⑤ $AC = BD$。能证明$\triangle ABC与\triangle DCB$全等的条件有几个？并选择其中一个进行证明。

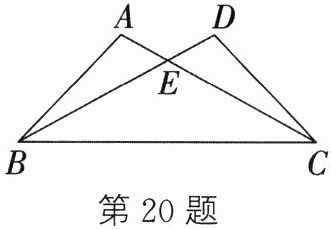
答案： ①②④ 证明：①：在$\triangle AEB$与$\triangle DEC$中，$\because \angle A = \angle D$，$AE = DE$，$\angle AEB = \angle DEC$，$\therefore \triangle AEB \cong \triangle DEC$，$\therefore BE = CE$，$\therefore \angle ACB = \angle DBC$。在$\triangle ABC$与$\triangle DCB$中，$\because \angle A = \angle D$，$\angle EBC = \angle ECB$，$BC = CB$，$\therefore \triangle ABC \cong \triangle DCB$；②：$\because BE = CE$，$\angle EBC = \angle ECB$。在$\triangle ABC$与$\triangle DCB$中，$\because \angle A = \angle D$，$\angle EBC = \angle ECB$，$BC = CB$，$\therefore \triangle ABC \cong \triangle DCB$；④：在$\triangle ABC$与$\triangle DCB$中，$\because \angle A = \angle D$，$BC = CB$，$\angle ABC = \angle DCB$，$\therefore \triangle ABC \cong \triangle DCB$。

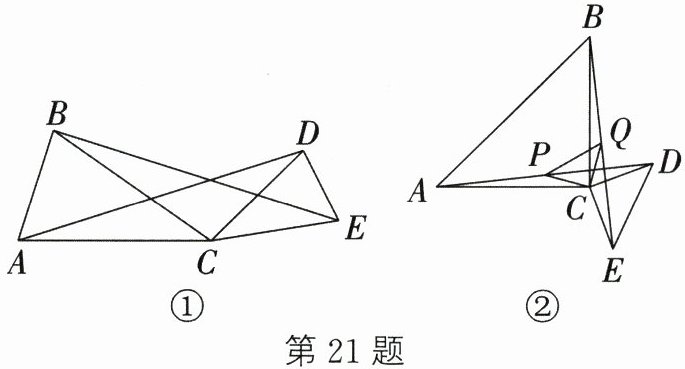
21.如图①,$CA = CB$,$CD = CE$,$\angle ACB= \angle DCE= \alpha$。
(1)求证：$BE = AD$；
(2)当$\alpha = 90^{\circ}$时,分别取AD、BE的中点P、Q,连接CP、CQ、PQ,如图②,判断$\triangle CPQ$的形状,并加以证明。

答案： （1）证明：$\because \angle ACB = \angle DCE = \alpha$，$\therefore \angle ACD = \angle BCE$。在$\triangle ACD$和$\triangle BCE$中，$\begin{cases}CA = CB\\\angle ACD = \angle BCE\\CD = CE\end{cases}$，$\therefore \triangle ACD \cong \triangle BCE(SAS)$，$\therefore BE = AD$；（2）$\triangle CPQ$为等腰直角三角形。证明：由（1）可得，$BE = AD$，$\because AD$、$BE$的中点分别为点$P$、$Q$，$\therefore AP = BQ$。$\because \triangle ACD \cong \triangle BCE$，$\therefore \angle CAP = \angle CBQ$。在$\triangle ACP$和$\triangle BCQ$中，$\begin{cases}CA = CB\\\angle CAP = \angle CBQ\\AP = BQ\end{cases}$，$\therefore \triangle ACP \cong \triangle BCQ(SAS)$，$\therefore CP = CQ$，且$\angle ACP = \angle BCQ$。又$\because \angle ACP + \angle PCB = 90^{\circ}$，$\therefore \angle BCQ + \angle PCB = 90^{\circ}$，$\therefore \angle PCQ = 90^{\circ}$，$\therefore \triangle CPQ$为等腰直角三角形。

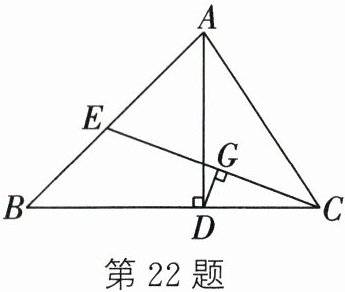
22.如图,在$\triangle ABC$中,AD是高,CE是中线,$DC = BE$,$DG\perp CE$于G。求证：
(1)G是CE的中点；
(2)$\angle B = 2\angle BCE$。

答案： 解：证明：（1）连接$DE$。$\because AD$是高，$CE$是中线，$\therefore DE = BE$。$\because DC = BE$，$\therefore DE = DC$。$\because DG \perp CE$，$\therefore G$是$CE$的中点；（2）$\because DE = BE$，$\therefore \angle B = \angle BDE$。$\because DE = DC$，$\therefore \angle DEC = \angle DCE$。$\because \angle BDE = \angle DEC + \angle DCE = 2\angle BCE$，$\therefore \angle B = 2\angle BCE$。