《2025年轻松作业本八年级数学上册苏科版》

19. 已知$y= y_1-y_2$,且$y_1与x$成正比例,$y_2与x-2$成正比例.当$x= 1$时,$y= 8$;当$x= -2$时,$y= 2$.求:
(1) $y与x$之间的函数表达式;
(2) 当$x$为何值时,$x= y$?

答案：
(1) $y = 2x + 6$
(2) $x = -6$时，$x = y$

20. 如图,在平面直角坐标系中,$\triangle ABC的三个顶点坐标分别为A(1,1)$,$B(5,2)$,$C(2,2)$.将点$A$、$C$分别向下平移3个单位长度得到点$A'$、$C'$.
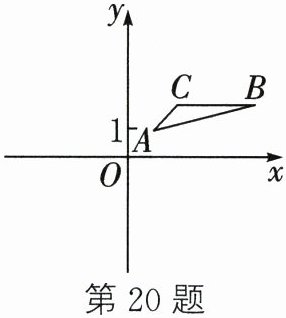
(1) 点$A'$、$C'$的坐标分别为$(1,-2)$,$(2,-1)$;
(2) 求证:点$A'$、$C'$、$B$在一条直线上.

答案：
(1) 解：$(1,-2),(2,-1)$；
(2) 证明：设直线$A'C'$的表达式为$y = kx + b$，$\therefore\begin{cases}k + b = -2\\2k + b = -1\end{cases}$，解得$\begin{cases}k = 1\\b = -3\end{cases}$，$\therefore$ 直线$A'C'$的表达式为$y = x - 3$，当$x = 5$时，$y = 5 - 3 = 2$。$\therefore$ 点$A'$、$C'$、$B$在一条直线上。

21. 已知一次函数$y_1= kx+2$($k$为常数,$k\neq0$)和$y_2= x-3$.
(1) 当$k= -2$时,若$y_1＞y_2$,求$x$的取值范围;
(2) 当$x＜1$时,$y_1＞y_2$.结合图象,直接写出$k$的取值范围.

答案：
解：
(1) 当$k = -2$时，$y_1 = -2x + 2$。根据题意，得$-2x + 2 ＞ x - 3$，解得$x ＜ \frac{5}{3}$；
(2) $-4 \leq k \leq 1$且$k \neq 0$。如图，直线$y_2 = x - 3$上横坐标是1的点$D$的纵坐标是-2。① 当直线$y_1 = kx + 2$经过点$D(1,-2)$时，$k = -4$。此时符合题意；② 当直线$y_1 = kx + 2$与直线$y_2 = x - 3$平行时，$k = 1$。此时符合题意；③ 当直线$y_1 = kx + 2$与直线$y_2 = x - 3$的交点$P$在射线$DC$上时，符合题意，此时$k$的取值范围是$-4 ＜ k ＜ 1$且$k \neq 0$。综上所述，$k$的取值范围是$-4 \leq k \leq 1$且$k \neq 0$。

22. 小明一家驱车从上海沿沪蓉高速回镇江,上海上车地离沪蓉高速镇江西出口的路程$y$(km)与所花时间$x$(h)之间的函数关系如图所示,结合图象,回答问题:
(1) 小明一家在$AB$段的速度是______60km/h;
(2) 小明一家从上海上车到镇江西高速出口,路上所花的时间为______3.2h;
(3) 小明说:“我们在高速上有一段连续1h恰好走了76km.”你认为有可能吗? 若有,请求出这1个小时的起止时间;若没有,请说明理由.
有可能：设这一个小时的开始时间为$t$，由小明一家在$AB$段的速度是$60\mathrm{km/h}$，可得$y_{AB} = -60x + 280$，设$BC$段的函数表达式为$y = kx + b$，根据题意得：$\begin{cases}k + b = 220\\2k + b = 120\end{cases}$，解得$\begin{cases}k = -100\\b = 320\end{cases}$，$\therefore y_{BC} = -100x + 320$；则$-60t + 280 - [-100(t + 1) + 320] = 76$，解得$t = 0.4$，即这1小时的起止时间为$0.4 \sim 1.4$小时。

答案： 解：
(1) 60
(2) 3.2
(3) 有可能：设这一个小时的开始时间为$t$，由小明一家在$AB$段的速度是$60\mathrm{km/h}$，可得$y_{AB} = -60x + 280$，设$BC$段的函数表达式为$y = kx + b$，根据题意得：$\begin{cases}k + b = 220\\2k + b = 120\end{cases}$，解得$\begin{cases}k = -100\\b = 320\end{cases}$，$\therefore y_{BC} = -100x + 320$；则$-60t + 280 - [-100(t + 1) + 320] = 76$，解得$t = 0.4$，即这1小时的起止时间为$0.4 \sim 1.4$小时。