19. 下图中的正方形网格,每个正方形顶点叫格点,请在图中画一个面积为10的正方形(每个正方形的边长为1).
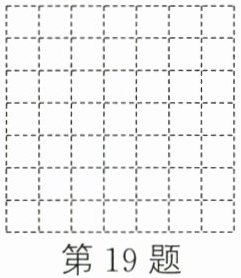

答案:
如图所示

如图所示

20. 如图,$\triangle ABC$中,$∠C= 90^{\circ}$,$AC= 4$,$BC= 8$.
(1) 用直尺和圆规作$AB$的垂直平分线(保留作图痕迹,不要求写作法);
(2) 若(1)中所作的垂直平分线交$BC于点D$,求$BD$的长.
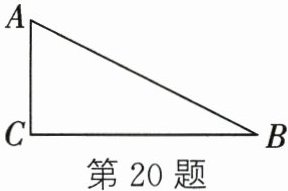
(1) 用直尺和圆规作$AB$的垂直平分线(保留作图痕迹,不要求写作法);
(2) 若(1)中所作的垂直平分线交$BC于点D$,求$BD$的长.

答案:
解:
(1) 所作AB的垂直平分线如图;
(2) 由作图可知$ AD = BD $,设$ BD = x $,则$ CD = (8 - x) $,$ \because ∠C = 90^{\circ} $,$ AC = 4 $,$ BC = 8 $,$ \therefore $由勾股定理可得:$ AC^{2} + CD^{2} = AD^{2} $。$ \therefore 4^{2} + (8 - x)^{2} = x^{2} $,解得$ x = 5 $。$ \therefore BD = 5 $。

解:
(1) 所作AB的垂直平分线如图;
(2) 由作图可知$ AD = BD $,设$ BD = x $,则$ CD = (8 - x) $,$ \because ∠C = 90^{\circ} $,$ AC = 4 $,$ BC = 8 $,$ \therefore $由勾股定理可得:$ AC^{2} + CD^{2} = AD^{2} $。$ \therefore 4^{2} + (8 - x)^{2} = x^{2} $,解得$ x = 5 $。$ \therefore BD = 5 $。

21. 如图,$OA\perp OB$,$OA= 45$海里,$OB= 15$海里,钓鱼岛位于点$O$处,我国海监船在点$B$处发现有一不明国籍的渔船,自$A点出发沿着AO方向匀速驶向钓鱼岛所在地点O$,我国海监船立即从$B$处出发以相同的速度沿直线去拦截这艘渔船,结果在点$C$处截住了渔船.
(1) 请用直尺和圆规作出$C$处的位置;
(2) 求我国海监船行驶的航程$BC$的长.

(1) 请用直尺和圆规作出$C$处的位置;
(2) 求我国海监船行驶的航程$BC$的长.

答案:
解:
(1) 作AB的垂直平分线与OA交于点C;
(2) 设BC为x海里,则CA也为x海里,$ \because ∠O = 90^{\circ} $,$ \therefore $在$ Rt△OBC $中,$ BO^{2} + OC^{2} = BC^{2} $,即$ 15^{2} + (45 - x)^{2} = x^{2} $,解得$ x = 25 $。$ \therefore $我国海监船行驶的航程BC的长为25海里。

解:
(1) 作AB的垂直平分线与OA交于点C;
(2) 设BC为x海里,则CA也为x海里,$ \because ∠O = 90^{\circ} $,$ \therefore $在$ Rt△OBC $中,$ BO^{2} + OC^{2} = BC^{2} $,即$ 15^{2} + (45 - x)^{2} = x^{2} $,解得$ x = 25 $。$ \therefore $我国海监船行驶的航程BC的长为25海里。

查看更多完整答案,请扫码查看


