《2025年实验班提优训练暑假衔接版七升八数学浙教版》

22. 一队学生从学校步行前往工厂参观,速度为 5 千米/小时,当走了 1 小时后,一名学生回校取东西,他以 7.5 千米/小时的速度回学校,取了东西后(取东西的时间不计)立即以同样的速度追赶队伍,结果在离工厂 2.5 千米处追上队伍. 求该校到工厂的路程.

答案： 27.5千米

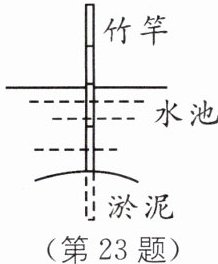
23. 新情境 利用竹竿测水深 一根竹竿插入一水池底部的淤泥中(如图),竹竿的入泥部分占全长的 $ \frac { 1 } { 5 } $. 淤泥以上的入水部分比入泥部分长 $ \frac { 1 } { 2 } $ 米,露出水面部分为 $ \frac { 13 } { 10 } $ 米,竹竿有多长？水有多深？

答案： 设竹竿的长为x米，则竹竿入泥部分为$\frac{1}{5}$x米,淤泥以上的入水部分为($\frac{1}{5}$x+$\frac{1}{2}$)米
由题意，得$\frac{1}{5}$x+$\frac{1}{5}$x+$\frac{1}{2}$+$\frac{13}{10}$=x,
解得x=3,则$\frac{1}{5}$x+$\frac{1}{2}$=$\frac{11}{10}$.
故竹竿的长为3米，水深为$\frac{11}{10}$米.
　二易错警示此类问题容易出错的地方是找不出题目中的等量关系，或者将未知量代表的数弄错，导致错解.

24. 毕业在即,九年级某班为纪念师生情谊,班委决定花 800 元班费买两种不同单价的留念册,分别给 50 位同学和 10 位任课老师每人一本留做纪念. 其中送给任课老师的留念册的单价比给同学的单价多 8 元. 请问这两种不同留念册的单价分别为多少元？

答案： 设送给任课老师的留念册的单价为x元,
　根据题意,得10x+50(x−8)=800,
　解得x=20,x−8=12(元).
　故送给任课老师的留念册的单价为20元，送给同学的留念册的单价为12元.

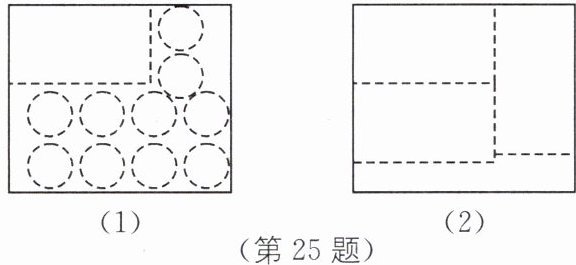
25. 新情境 定制客机模型礼盒 某工厂现需为 C919 客机模型制作一款定制礼盒,工作人员准备按照以下两种裁剪方式制作,已知 1 个长方形和 2 个圆可以组装成 1 个礼盒,现有 210 张纸板,其中 $ a $ 张纸板用图(1)的方式裁剪,剩余纸板用图(2)的方式裁剪.
(1)若组装完后,裁出的圆形和长方形正好用完,则一共做了多少个礼盒？
(2)如果按照上面的方式,一共要做 550 个礼盒,则至少还需要增加多少张纸板？

答案：
(1)根据题意,得a+3(210−a)=$\frac{1}{2}$×10a,
　　即630−2a=5a,解得a=90,
∴共有90张纸板用题图
(1)方式裁剪，共裁出900个圆
　
∵每个礼盒需要两个圆，900÷2=450(个).
　故共做了450个礼盒.
(2)
∵一共要做550个礼盒，由
(1)，知还需要制作550−450=100(个)礼盒，
　则还需要裁出200个圆形和100个长方形，
　
∴用题图
(1)的方式裁剪所需要的圆的纸板数量为200÷10=20(张).
　
∵使用的纸板数量要最少，
　
∴剩余长方形均用题图
(2)的方式裁剪，需要的纸板数量为(100−20)÷3=26$\frac{2}{3}$(张).
　
∴至少还需纸板20+26+1=47(张).
　故至少还需要增加47张纸板.
　归纳总结本题考查的是一元一次方程的应用，理解题意，确定相等关系建立方程是解本题的关键,