2025年实验班提优训练暑假衔接版七升八数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版七升八数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
20. 解下列方程或方程组:
(1)$\left\{\begin{array}{l} 4s+3t= 5,\\ 2s-t= 5;\end{array}\right. $
(2)$\frac {3x+2}{x+1}= \frac {x-2}{3x+3}-\frac {2}{3}$.
(1)$\left\{\begin{array}{l} 4s+3t= 5,\\ 2s-t= 5;\end{array}\right. $
(2)$\frac {3x+2}{x+1}= \frac {x-2}{3x+3}-\frac {2}{3}$.
答案:
(1) $\begin{cases}4s + 3t = 5, ①\\2s - t = 5, ②\end{cases}$
由②,得 t = 2s - 5,③
把③代入①,得 4s + 3(2s - 5) = 5,解得 s = 2
把 s = 2 代入③,得 t = -1
所以原方程组的解为 $\begin{cases}s = 2,\\t = -1.\end{cases}$
(2) 去分母,得 9x + 6 = x - 2 - 2(x + 1)
整理,得 10x = -10,解得 x = -1
经检验,x = -1 是增根
所以分式方程无解
(1) $\begin{cases}4s + 3t = 5, ①\\2s - t = 5, ②\end{cases}$
由②,得 t = 2s - 5,③
把③代入①,得 4s + 3(2s - 5) = 5,解得 s = 2
把 s = 2 代入③,得 t = -1
所以原方程组的解为 $\begin{cases}s = 2,\\t = -1.\end{cases}$
(2) 去分母,得 9x + 6 = x - 2 - 2(x + 1)
整理,得 10x = -10,解得 x = -1
经检验,x = -1 是增根
所以分式方程无解
21. 如图,在$△ABC$中,E是CA延长线上一点,$AD⊥BC$于点D,$EG⊥BC$于点G,$∠E= ∠3$. 求证:$∠1= ∠2$.
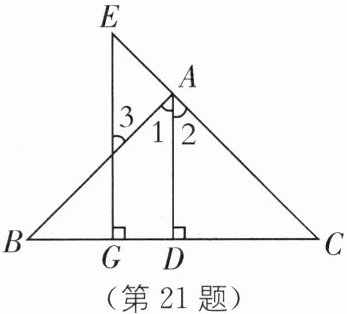

答案:
∵ AD ⊥ BC,EG ⊥ BC,
∴ ∠EGC = ∠ADC = 90°,
∴ EG // AD,
∴ ∠2 = ∠E,∠1 = ∠3
∵ ∠E = ∠3,
∴ ∠1 = ∠2
方法诠释 本题主要考查了平行线的性质及判定,综合运用平行线的性质和判定定理是解答此题的关键
∵ AD ⊥ BC,EG ⊥ BC,
∴ ∠EGC = ∠ADC = 90°,
∴ EG // AD,
∴ ∠2 = ∠E,∠1 = ∠3
∵ ∠E = ∠3,
∴ ∠1 = ∠2
方法诠释 本题主要考查了平行线的性质及判定,综合运用平行线的性质和判定定理是解答此题的关键
22. 如图,在四边形ABCD中,点M,N分别在AB,BC上,将$△BMN$沿MN翻折,得$△FMN$,若$MF// AD$,$FN// DC$,则$∠B$是多少?(提示:图边形内角和为$360^{\circ }$)
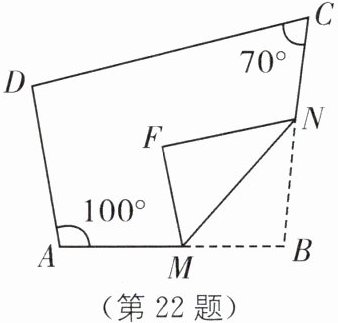

答案:
∵ FN // DC,MF // AD,
∴ ∠BNF = ∠C = 70°,∠BMF = ∠A = 100°
∵ ∠BMF + ∠B + ∠BNF + ∠F = 360°,
∴ ∠B + ∠F = 190°
又 ∠B = ∠F,
∴ ∠F = ∠B = 95°
∵ FN // DC,MF // AD,
∴ ∠BNF = ∠C = 70°,∠BMF = ∠A = 100°
∵ ∠BMF + ∠B + ∠BNF + ∠F = 360°,
∴ ∠B + ∠F = 190°
又 ∠B = ∠F,
∴ ∠F = ∠B = 95°
23. 某旅游公司为了了解我市“4A”级景区的知名度情况,特对部分市民进行现场采访,根据市民对13个景区名字的回答情况,分为熟悉(A)、基本了解(B)、略有知晓(C)、知之甚少(D)四类进行统计,绘制了两幅统计图(不完整),请根据图中信息解答下列问题:
(1)本次调查活动的样本容量为____.
(2)本次调查中属于“基本了解”的市民有____人.
(3)补全条形统计图.
(4)“略有知晓”类占扇形统计图的圆心角是多少度?“知之甚少”类市民占被调查人数的百分比是多少?
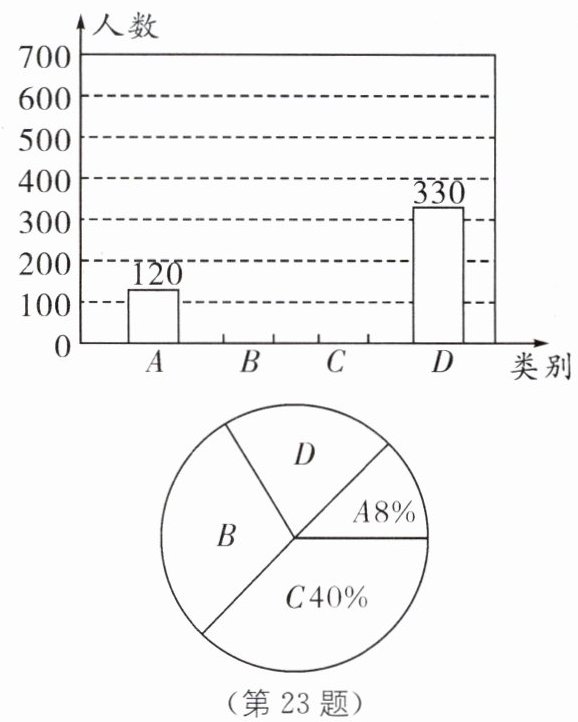
(1)本次调查活动的样本容量为____.
(2)本次调查中属于“基本了解”的市民有____人.
(3)补全条形统计图.
(4)“略有知晓”类占扇形统计图的圆心角是多少度?“知之甚少”类市民占被调查人数的百分比是多少?

答案:
(1) 1500
(2) 450
(3) 补全统计图如图所示:

(4) “略有知晓”类:360°×40% = 144°,
“知之甚少”类占 $\frac{330}{1500}×100\% = 22\%$
故“略有知晓”类占扇形统计图的圆心角是 144°,“知之甚少”类市民占被调查人数的 22%
(1) 1500
(2) 450
(3) 补全统计图如图所示:

(4) “略有知晓”类:360°×40% = 144°,
“知之甚少”类占 $\frac{330}{1500}×100\% = 22\%$
故“略有知晓”类占扇形统计图的圆心角是 144°,“知之甚少”类市民占被调查人数的 22%
查看更多完整答案,请扫码查看


