2025年实验班提优训练暑假衔接版七升八数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版七升八数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
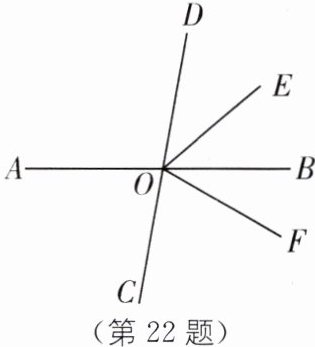
22. 如图,已知直线AB,CD相交于点O,OE平分$∠BOD$,OF平分$∠COE$。若$∠AOD= 100^{\circ }$,求:
(1)$∠EOD$的度数;
(2)$∠AOF$的度数。
(1)$∠EOD$的度数;
(2)$∠AOF$的度数。

答案:
(1)
∵直线AB,CD相交于O,
∴∠AOD+∠BOD=180°,
∵∠AOD=100°,
∴∠BOD=180°−∠AOD=80°.
∵OE平分∠BOD,
∴∠EOD=$\frac{1}{2}$∠BOD=40°.
(2)
∵∠COE+∠EOD=180°,
∴∠COE=180°−∠EOD=140°.
∵OF平分∠COE,
∴∠COF=$\frac{1}{2}$∠COE=70°.
∵∠AOC=∠BOD=80°,
∴∠AOF=∠AOC+∠COF=150°.
(1)
∵直线AB,CD相交于O,
∴∠AOD+∠BOD=180°,
∵∠AOD=100°,
∴∠BOD=180°−∠AOD=80°.
∵OE平分∠BOD,
∴∠EOD=$\frac{1}{2}$∠BOD=40°.
(2)
∵∠COE+∠EOD=180°,
∴∠COE=180°−∠EOD=140°.
∵OF平分∠COE,
∴∠COF=$\frac{1}{2}$∠COE=70°.
∵∠AOC=∠BOD=80°,
∴∠AOF=∠AOC+∠COF=150°.
23. 如图,$CB⊥AB$于点B,CE平分$∠DCB$,DE平分$∠CDA$,$∠EDC+∠ECD= 90^{\circ }$,试说明AD与AB是否垂直。


答案:
∵CE平分∠DCB,DE平分∠CDA,
∴∠ADC=2∠EDC,∠BCD=2∠ECD.
∵∠EDC+∠ECD=90°,
∴∠ADC+∠BCD=180°,
∴AD//BC.
∵CB⊥AB,
∴AD⊥AB.
∵CE平分∠DCB,DE平分∠CDA,
∴∠ADC=2∠EDC,∠BCD=2∠ECD.
∵∠EDC+∠ECD=90°,
∴∠ADC+∠BCD=180°,
∴AD//BC.
∵CB⊥AB,
∴AD⊥AB.
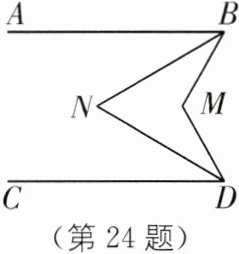
24. 如图,$AB// CD$,BN,DN分别平分$∠ABM$,$∠MDC$,试问:$∠BMD$,$∠N$之间的数量关系如何?并说明理由。

答案:
∠BMD=2∠N.理由如下:
如图,过点M作ME//AB.

∵AB//CD,
∴ME//CD.
∴∠ABM=∠BME,∠CDM=∠DME.
∴∠BMD=∠BME+∠DME=∠ABM+∠CDM;同理,可得∠N=∠ABN+∠CDN=$\frac{1}{2}$∠ABM+$\frac{1}{2}$∠CDM=$\frac{1}{2}$(∠ABM+∠CDM),
∴∠BMD=2∠N.
∠BMD=2∠N.理由如下:
如图,过点M作ME//AB.

∵AB//CD,
∴ME//CD.
∴∠ABM=∠BME,∠CDM=∠DME.
∴∠BMD=∠BME+∠DME=∠ABM+∠CDM;同理,可得∠N=∠ABN+∠CDN=$\frac{1}{2}$∠ABM+$\frac{1}{2}$∠CDM=$\frac{1}{2}$(∠ABM+∠CDM),
∴∠BMD=2∠N.
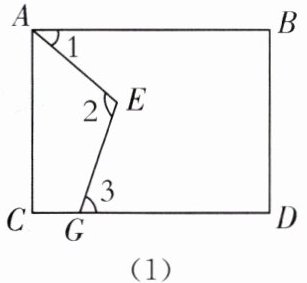
25. 中考新考法 归纳一般结论 将图(1)中的长方形纸片任意剪两刀,可以得到$∠2$与$∠1$,$∠3$有什么关系?
将图(2)中的长方形纸片任意剪四刀,可以得到$∠1$,$∠3$,$∠5$与$∠2$,$∠4$有什么关系?
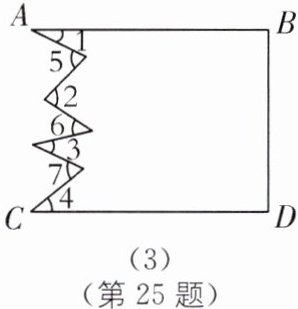
将图(3)中的长方形纸片任意剪六刀,可以得到$∠1$,$∠2$,$∠3$,$∠4$,$∠5$,$∠6$,$∠7$之间有什么关系?
将长方形纸片任意剪n刀,你会发现什么规律?

将图(2)中的长方形纸片任意剪四刀,可以得到$∠1$,$∠3$,$∠5$与$∠2$,$∠4$有什么关系?
将图(3)中的长方形纸片任意剪六刀,可以得到$∠1$,$∠2$,$∠3$,$∠4$,$∠5$,$∠6$,$∠7$之间有什么关系?
将长方形纸片任意剪n刀,你会发现什么规律?



答案:
在图
(1)中,过点E作EF//AB,交AC于点F,则有EF//AB//CD.
因为AB//EF,所以∠1=∠AEF.
同理∠3=∠GEF.
所以∠1+∠3=∠AEF+∠GEF=∠2,
即∠2=∠1+∠3.
同样的作法,在图
(2)中过点E,F,G分别作AB的平行线,同理可得∠1+∠3+∠5=∠2+∠4,在图
(3)中,同样可得∠1+∠2+∠3+∠4=∠5+∠6+∠7.
规律:两平行线间的折线所成的角之间的关系:向右方向的角之和等于向左方向的角之和.
(1)中,过点E作EF//AB,交AC于点F,则有EF//AB//CD.
因为AB//EF,所以∠1=∠AEF.
同理∠3=∠GEF.
所以∠1+∠3=∠AEF+∠GEF=∠2,
即∠2=∠1+∠3.
同样的作法,在图
(2)中过点E,F,G分别作AB的平行线,同理可得∠1+∠3+∠5=∠2+∠4,在图
(3)中,同样可得∠1+∠2+∠3+∠4=∠5+∠6+∠7.
规律:两平行线间的折线所成的角之间的关系:向右方向的角之和等于向左方向的角之和.
查看更多完整答案,请扫码查看


