《2025年通城学典活页检测八年级数学下册浙教版》

1. 用配方法解3x² + 6x - 1 = 0时，将它化为(x + a)² = b的形式，则a + b的值为 ( )
A. $\frac{10}{3}$
B. $\frac{7}{3}$
C. 2
D. $\frac{4}{3}$

答案： B

2. 若一个一元二次方程的二次项是2x²，配方整理后，得$(x - \frac{3}{2})² = \frac{3}{4}$，则它的一次项和常数项分别是 ( )
A. -3x,3
B. -3x,$\frac{3}{2}$
C. -6x,$\frac{3}{2}$
D. -6x,3

答案： D

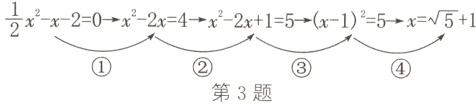
3. 如图，下列用配方法解方程$\frac{1}{2}x² - x - 2 = 0$的四个步骤中，开始出现错误的步骤是 ( )
$\frac{1}{2}x² - x - 2 = 0 \to x² - 2x = 4 \to x² - 2x + 1 = 5 \to (x - 1)² = 5 \to x = \sqrt{5} + 1$
① ② ③ ④
　　　　　　　　　　
A. ①
B. ②
C. ③
D. ④

答案： D

4. 若方程4x² - (m - 2)x + 1 = 0的左边可以写成完全平方式，则m的值为 ( )
A. -2
B. -2或6
C. -2或-6
D. 2或-6

答案： B

5. 将一元二次方程4x² - 4x - 3 = 0配方后，得$(x - \frac{1}{2})² =$_______.

答案： 1

6. 对方程5x² + 2x - 3 = 0进行配方，得$x² + \frac{2}{5}x + m = \frac{3}{5} + m$，其中m = _______.

答案： $\frac{1}{25}$

7. 用配方法解一元二次方程2x² - 5x - 3 = 0，可以写成(x + h)² = k的形式，则k - h = _______.

答案： $\frac{69}{16}$

8. 当x = __________时，代数式3x² - 6x的值为12.

答案： $1+\sqrt{5}$或$1-\sqrt{5}$

9. 如果x = 0是关于x的一元二次方程(m - 2)x² + 3x + 3m² - 5m - 2 = 0的一个根，那么m = _______.

答案： $-\frac{1}{3}$

10. (24分)用配方法解下列方程：
(1) 2x² - 4x = 3; (2) 3x² - 6x - 1 = 0;
(3) 2x² = 7 + 6x; (4) -$\frac{5}{4}x = \frac{7}{4} - \frac{1}{2}x²$.

答案： （1）整理，得$x^{2}-2x=\frac{3}{2}$。方程的两边同加上1，得$x^{2}-2x + 1=\frac{3}{2}+1$，即$(x - 1)^{2}=\frac{5}{2}$。则$x - 1=\frac{\sqrt{10}}{2}$或$x - 1=-\frac{\sqrt{10}}{2}$，解得$x_{1}=1+\frac{\sqrt{10}}{2},x_{2}=1-\frac{\sqrt{10}}{2}$
（2）整理，得$x^{2}-2x=\frac{1}{3}$。方程的两边同加上1，得$x^{2}-2x + 1=\frac{1}{3}+1$，即$(x - 1)^{2}=\frac{4}{3}$。则$x - 1=\frac{2\sqrt{3}}{3}$或$x - 1=-\frac{2\sqrt{3}}{3}$，解得$x_{1}=1+\frac{2\sqrt{3}}{3},x_{2}=1-\frac{2\sqrt{3}}{3}$
（3）整理，得$x^{2}-3x=\frac{7}{2}$。方程的两边同加上$\frac{9}{4}$，得$x^{2}-3x+\frac{9}{4}=\frac{7}{2}+\frac{9}{4}$，即$(x-\frac{3}{2})^{2}=\frac{23}{4}$。则$x-\frac{3}{2}=\frac{\sqrt{23}}{2}$或$x-\frac{3}{2}=-\frac{\sqrt{23}}{2}$，解得$x_{1}=\frac{3+\sqrt{23}}{2},x_{2}=\frac{3-\sqrt{23}}{2}$
（4）整理，得$x^{2}-\frac{5}{2}x=\frac{7}{2}$。方程的两边同加上$\frac{25}{16}$，得$x^{2}-\frac{5}{2}x+\frac{25}{16}=\frac{7}{2}+\frac{25}{16}$，即$(x - \frac{5}{4})^{2}=\frac{81}{16}$。则$x-\frac{5}{4}=\frac{9}{4}$或$x-\frac{5}{4}=-\frac{9}{4}$，解得$x_{1}=\frac{7}{2},x_{2}=-1$