《2025年名校课堂内外五年级数学下册人教版》

一 用棱长 1cm 的小正方体拼成如下的大正方体后，把它们的表面分别涂上颜色。在①、②、③中，三面、两面、一面涂色以及没有涂色的小正方体各有多少块？


按这样的规律摆下去，第④、⑤个大正方体的结果会是怎样？

由以上可知，涂色情况与正方体的( )有关。当棱长为 $n\mathrm{cm}(n\geqslant2)$时：

答案：
棱长@@8@@$12(n - 2)$@@$6(n - 2)^2$@@$(n - 2)^3$

二 数一数下面的图形中有多少个小正方体？

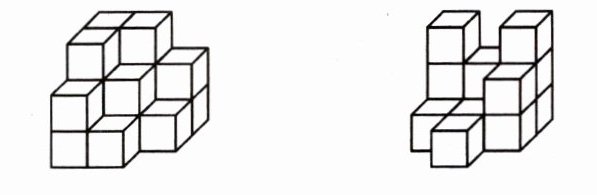
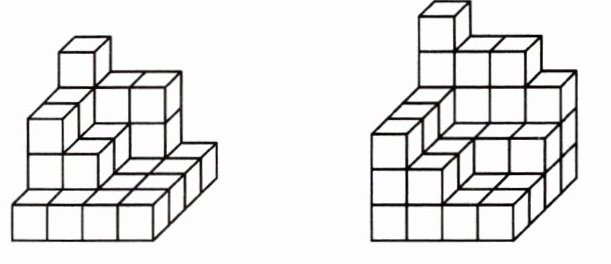
( )个 ( )个

( )个 ( )个

答案： 17 13 29 39

三 现有一个长 5cm、宽 4cm、高 3cm 的长方体木块，先在它的六个面上都涂上红色，然后把它锯成棱长为 1cm 的小正方体木块。在锯成的小正方体木块中，三面涂有红色的有多少块？两面涂有红色的有多少块？一面呢？没有涂色的呢？

答案： 三面：$1×8 = 8$（块） 两面：$(5 - 2)×4+(4 - 2)×4+(3 - 2)×4 = 24$（块） 一面：$[(5 - 2)×(4 - 2)+(5 - 2)×(3 - 2)+(4 - 2)×(3 - 2)]×2 = 22$（块） 没有涂色：$5×4×3 - 8 - 24 - 22 = 6$（块） 答：三面涂有红色的有8块，两面涂有红色的有24块，一面涂有红色的有22块，没有涂色的有6块。