《2025年学霸三年级数学下册苏教版》

4. 下面的字母或汉字各表示什么数字？

答案：
9 3 3 8 提示：第一个竖式：根据“好学×好=□学7”可知，学、好可能是9和3。根据“好学×学=□好”可知，好=9，学=3。第二个竖式：根据“AB×A = 114”及“A×A+ = 11”，可知A = 3，那么B = 8。

例3 在计算一道两位数乘两位数的乘法算式时，错把其中一个乘数23个位上的3看成了8，算出的结果比正确的结果多245，正确的答案是多少？
分析：一个乘数是23，就说明是一个数乘23，积就是这个数的23倍。把23个位上的3看成8，就是多加了这个数的$(8 - 3)$倍，积多了245，也就是这个数的$(8 - 3)$倍是245，据此可求出这个数，再乘23求出正确的答案。
解答：$8 - 3 = 5$ $245\div5 = 49$
$49\times23 = 1127$

答案：

5. 周梅在计算一道两位数乘两位数的乘法算式时，错把其中一个乘数59个位上的9看成了6，算出的结果比正确的结果少171，正确的答案是( )。

答案： 3363 提示：把乘数59个位上的9看成了6，这个乘数小了9 - 6 = 3，算出的结果比正确的结果少171，即另一个乘数为171÷3 = 57，所以正确的答案是57×59 = 3363。

6. 小明在做两位数乘两位数的计算题时，忘记添上后面的一个0了，算出的积比正确的积少774。正确的积应该是多少？

答案： 10 - 1 = 9 774÷9 = 86 86×10 = 860 提示：根据“忘记添上后面的一个0”可以知道：正确的积是现在的10倍，如果把现在的积看作1份，那么正确的积就是10份。现在的积比正确的积少了10 - 1 = 9(份)，又知道“算出的积比正确的积少774”，用774÷9 = 86，算出现在的积是86，正确的积就是86×10 = 860。

7. 如图，一个两位数乘24，在计算十位上的2与这个两位数相乘时，错误地将所得的结果末位与个位对齐了，所得的结果是144。正确的结果是多少？

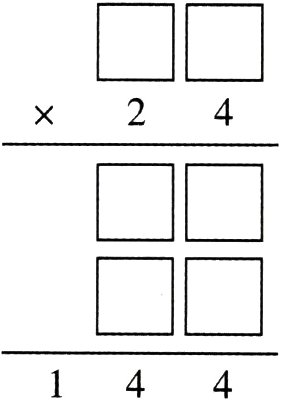
答案： 2 + 4 = 6 144÷6 = 24 24×24 = 576 提示：根据算理可知，第二步应该用24十位上的2与第一个乘数相乘，所得的结果末位与十位对齐，表示20个第一个乘数的和。如果末位与个位对齐，那么表示所得的结果是2个第一个乘数的和，这样最后的结果就是4个第一个乘数的和加2个第一个乘数的和，一共是6个第一个乘数的和。因为算得的结果是144，也就是6个第一个乘数的和是144，用除法求出这个乘数是144÷6 = 24，所以正确的结果是24×24 = 576。