2025年通成学典课时作业本高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通成学典课时作业本高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
16. (18分)某校化学课题组为改进某项实验技术,减少实验时间,从而提高实验效率,从该校高二化学社团选取40名学生,并将他们平均分成两个实验组.第一组学生用原方法做实验,第二组学生用新方法做实验.现统计两组同学完成实验的时间(单位:min)如下:
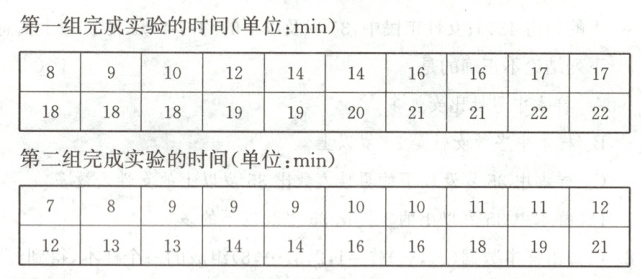
(1) 记这40名学生完成实验时间(单位:min)的中位数为$m$,根据上述信息完成如下实验方法和实验时间样本数据的$2×2$列联表(单位:min):

(2) 依据小概率值$\alpha=0.01$的独立性检验,分析新方法的实验效率是否比原方法高.
附:$\chi^{2}=\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中$n=a+b+c+d$.
临界值表:


(1) 记这40名学生完成实验时间(单位:min)的中位数为$m$,根据上述信息完成如下实验方法和实验时间样本数据的$2×2$列联表(单位:min):

(2) 依据小概率值$\alpha=0.01$的独立性检验,分析新方法的实验效率是否比原方法高.
附:$\chi^{2}=\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中$n=a+b+c+d$.
临界值表:

答案:
16.解:
(1)填表如下:
实验时间
实验方法 大于$m$ 不大于$m$ 合计
原方法 14 6 20
新方法 5 15 20
合计 19 21 40
(2)零假设为$H_{0}$:实验方法与实验效率无关.根据列联表,得$\chi^{2}=\frac{40 × (14 × 15-6 × 5)^{2}}{20 × 20 × 19 × 21} \approx 8.120>6.635=x_{0.01}$,所以根据小概率值$\alpha=0.01$的独立性检验,可推断$H_{0}$不成立,即实验方法与实验效率有关,此推断出错的概率不大于0.01.结合题表中的数据可知,新方法的实验效率比原方法高.
(1)填表如下:
实验时间
实验方法 大于$m$ 不大于$m$ 合计
原方法 14 6 20
新方法 5 15 20
合计 19 21 40
(2)零假设为$H_{0}$:实验方法与实验效率无关.根据列联表,得$\chi^{2}=\frac{40 × (14 × 15-6 × 5)^{2}}{20 × 20 × 19 × 21} \approx 8.120>6.635=x_{0.01}$,所以根据小概率值$\alpha=0.01$的独立性检验,可推断$H_{0}$不成立,即实验方法与实验效率有关,此推断出错的概率不大于0.01.结合题表中的数据可知,新方法的实验效率比原方法高.
17. (20分)小张准备在某商场租一间商铺开餐厅,为了解市场行情,在该商场调查了20家餐厅,统计得到了它们的面积$x$(单位:$\mathrm{m}^{2}$)和日均客流量$y$(单位:百人)的数据$(x_{i},y_{i})(i=1,2,·s,20)$,并计算得$\sum\limits_{i=1}^{20}x_{i}=2\ 400$,$\sum\limits_{i=1}^{20}y_{i}=210$,$\sum\limits_{i=1}^{20}(x_{i}-\overline{x})^{2}=42\ 000$,$\sum\limits_{i=1}^{20}(x_{i}-\overline{x})(y_{i}-\overline{y})=6\ 300$.
(1) 求$y$关于$x$的经验回归方程;
(2) 已知餐厅每天的经济效益$W=m\sqrt{y}+kx(k\gt0,m\gt0)$,该商场现有$80\sim150\mathrm{m}^{2}$的商铺出租,根据(1)的结果进行预测,要使单位面积的经济效益$Z$最高,小张应该租多大面积的商铺?
附:经验回归方程$\hat{y}=\hat{b}x+\hat{a}$中,$\hat{b}=\frac{\sum\limits_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum\limits_{i=1}^{n}(x_{i}-\overline{x})^{2}}$,$\hat{a}=\overline{y}-\hat{b}\overline{x}$.
(1) 求$y$关于$x$的经验回归方程;
(2) 已知餐厅每天的经济效益$W=m\sqrt{y}+kx(k\gt0,m\gt0)$,该商场现有$80\sim150\mathrm{m}^{2}$的商铺出租,根据(1)的结果进行预测,要使单位面积的经济效益$Z$最高,小张应该租多大面积的商铺?
附:经验回归方程$\hat{y}=\hat{b}x+\hat{a}$中,$\hat{b}=\frac{\sum\limits_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum\limits_{i=1}^{n}(x_{i}-\overline{x})^{2}}$,$\hat{a}=\overline{y}-\hat{b}\overline{x}$.
答案:
17.解:
(1)由已知,可得$\bar{x}=\frac{1}{20}\sum_{i=1}^{20}x_{i}=120$,$\bar{y}=\frac{1}{20}\sum_{i=1}^{20}y_{i}=10.5$,$\hat{b}=\frac{\sum_{i=1}^{20}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum_{i=1}^{20}(x_{i}-\bar{x})^{2}}=\frac{6300}{42000}=0.15$,则$a=\bar{y}-\hat{b}\bar{x}=10.5-0.15 × 120=-7.5$,所以$y$关于$x$的经验回归方程为$\hat{y}=0.15x-7.5$.
(2)根据题意,得$Z=\frac{W}{x}=m\frac{\sqrt{0.15x-7.5}}{x}+k(80 \leq x \leq 150)$.设$f(x)=\frac{\sqrt{0.15x-7.5}}{x}=\frac{\sqrt{0.15x-7.5}}{x^{2}}(80 \leq x \leq 150)$.令$t=\frac{1}{x}$,则$\frac{1}{150} \leq t \leq \frac{1}{80}$.令$g(t)=0.15t-7.5t^{2}=-7.5 × (t-\frac{0.01}{10})^{2}+0.000075$,易知当$t=0.01$时$g(t)$取得最大值,即当$x=100$时$f(x)$取得最大值.又因为$k>0$,$m>0$,所以此时$Z$也取得最大值.所以小张应该租$100m^{2}$的商铺.
(1)由已知,可得$\bar{x}=\frac{1}{20}\sum_{i=1}^{20}x_{i}=120$,$\bar{y}=\frac{1}{20}\sum_{i=1}^{20}y_{i}=10.5$,$\hat{b}=\frac{\sum_{i=1}^{20}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum_{i=1}^{20}(x_{i}-\bar{x})^{2}}=\frac{6300}{42000}=0.15$,则$a=\bar{y}-\hat{b}\bar{x}=10.5-0.15 × 120=-7.5$,所以$y$关于$x$的经验回归方程为$\hat{y}=0.15x-7.5$.
(2)根据题意,得$Z=\frac{W}{x}=m\frac{\sqrt{0.15x-7.5}}{x}+k(80 \leq x \leq 150)$.设$f(x)=\frac{\sqrt{0.15x-7.5}}{x}=\frac{\sqrt{0.15x-7.5}}{x^{2}}(80 \leq x \leq 150)$.令$t=\frac{1}{x}$,则$\frac{1}{150} \leq t \leq \frac{1}{80}$.令$g(t)=0.15t-7.5t^{2}=-7.5 × (t-\frac{0.01}{10})^{2}+0.000075$,易知当$t=0.01$时$g(t)$取得最大值,即当$x=100$时$f(x)$取得最大值.又因为$k>0$,$m>0$,所以此时$Z$也取得最大值.所以小张应该租$100m^{2}$的商铺.
查看更多完整答案,请扫码查看


