《2025年5年高考3年模拟高中物理选择性必修第三册人教版江苏专版》

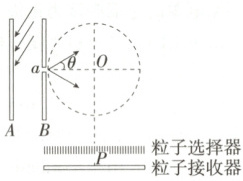
16.(16 分)如图为某同学设计的光电效应研究装置,A、B 为金属板,频率
为 $ν$的单色光照射到 A 板上发生光电效应,经 A、B 间的电场加速后,部
分光电子从小孔 $a$进入图中虚线所示的圆形匀强磁场区域,圆形匀强
磁场半径为 $R$,磁场区域的下方有一粒子选择器和一粒子接收器。$P$
在磁场圆心 $O$的正下方,$aO$与 $PO$垂直,粒子接收器与 $PO$垂直。光
电子经过电场加速后能从 $a$孔以不同的角度进入磁场,已知元电荷为 $e$,
电子的质量为 $m_0$,A、B 间的加速电压为 $U_0$,只有速度方向垂直于粒子
接收器的光电子才能通过粒子选择器,其他光电子被粒子选择器吸收
并立即导入大地,通过粒子选择器的光电子最终打在粒子接收器上,被
粒子接收器吸收并立即导入大地。重力忽略不计,不考虑光电子之间
的相互作用力,不考虑缓慢变化的磁场产生的电场,只考虑纸面内运
动的电子,普朗克常量为 $h$。
(1)磁感应强度 $B = B_0$时,某光电子从 A 板离开时的速度为 0,求该光电子经过 $a$进入磁场后做圆周运动的半径 $R_1$。
(2)光电子从 $a$孔进人时速度与 $aO$的夹角范围为 0°≤ $θ$ ≤ 30°,求粒子接收器上接收到光电子的长度 $L$。
(3)磁感应强度由 $B_0$缓慢增大到 $B_1$时,粒子接收器上恰好不能再接收到光电子,求金属 A 的逸出功 $W_0$。

答案： 16.答案
(1)$\frac{1}{B_{0}}\sqrt{\frac{2m_{0}U_{0}}{e}}$
(2)$R$
(3)$h\nu +eU_{0}-\frac{e^{2}B_{1}^{2}R^{2}}{2m_{0}}$
解析
(1)该光电子在电场中的加速过程，根据动能定理有$eU_{0}=\frac{1}{2}m_{0}v^{2}$
在磁场中，根据洛伦兹力提供向心力有$evB =m_{0}\frac{v^{2}}{R_{1}}$
联立解得$R_{1}=\frac{1}{B_{0}}\sqrt{\frac{2m_{0}U_{0}}{e}}$
(2)能打在粒子接收器上的光电子运动轨迹半径$r =R$
设$\theta=30^{\circ}$偏上进入的光电子打在$P$点右侧距离为$x$处，根据几何关系有$x=R\sin30^{\circ}=\frac{R}{2}$
$\theta=30^{\circ}$偏下进入的光电子打在$P$点左侧距离为$x'$处，有$x'=R\sin30^{\circ}=\frac{R}{2}$
粒子接收器上接收到光电子的长度$L=x'+x=R$
(3)当磁感应强度最大时，对应最大的入射速度，$v_{max}=\frac{eB_{1}R}{m_{0}}$
A板处发生光电效应逸出的光电子的最大初动能$E_{kmax}=h\nu -W_{0}=\frac{1}{2}m_{0}v_{0}^{2}$
经过电场加速后，根据动能定理可得$eU_{0}=\frac{1}{2}m_{0}v_{max}^{2}-\frac{1}{2}m_{0}v_{0}^{2}$
联立解得$W_{0}=h\nu +eU_{0}-\frac{e^{2}B_{1}^{2}R^{2}}{2m_{0}}$