《2025年直击考点冲刺100分六年级数学上册苏教版》

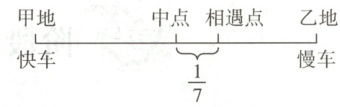
6. 如图,一列快车和一列慢车分别从甲、乙两地相对开出,3小时后相遇,相遇点与甲、乙两地中点的距离占全程的$\frac{1}{7}$。已知快车比慢车每小时多行驶60千米,求甲、乙两地之间的距离。(6分)

答案： 6. $3×60÷(2×\frac{1}{7})=630(千米)$

1. 一场演出的票价是180元一张,票价降低后观众人数比预计的增加一半,总收入比预计增加了$\frac{1}{6}$。一张演出票降价多少元?(提示:先假设预计的观众人数,再列式计算)(5分)

答案： 1. 假设预计的观众有1000人。 $1000×(1+\frac{1}{2})=1500(人)$ $180×1000×(1+\frac{1}{6})=210000(元)$ $180 - 210000÷1500 = 40(元)$

2. 3只猴子摘桃子,第1只猴子摘的桃子个数是其余两只猴子摘的桃子个数的$\frac{1}{2}$,第2只猴子摘的桃子个数是其余两只猴子摘的个数的$\frac{2}{7}$,第3只猴子摘了24个桃子。它们一共摘了多少个桃子?(5分)

答案： 2. $24÷(1 - \frac{1}{1 + 2}-\frac{2}{2 + 7})=54(个)$ 提示:第1只猴子摘的个数是其余两只猴子摘的桃子个数的$\frac{1}{2}$,说明第1只猴子摘的桃子个数占总个数的$\frac{1}{1 + 2}=\frac{1}{3}$,同理,第2只猴子摘的桃子个数占总个数的$\frac{2}{2 + 7}=\frac{2}{9}$,所以第3只猴子摘的桃子个数占总个数的$1-\frac{1}{3}-\frac{2}{9}=\frac{4}{9}$,进而求解。