《2025年小题狂做高中物理必修第二册人教版巅峰版》

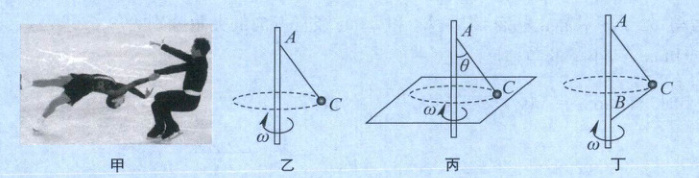
例 1 (2024 山东济宁期中)2022 年北京冬奥会上，中国花样滑冰队不负众望，在双人滑项目上强势夺冠，这也是中国队时隔$12$年之后再次登上奥运会最高领奖台。该项目有一项技术动作叫双人螺旋线，如图甲所示，以男选手为轴心，女选手围绕男选手旋转。将这一情景抽象成如图乙所示的模型，一细线一端系住一小球，另一端固定在一竖直细杆上，小球以一定大小的速度随着细杆在水平面内做匀速圆周运动，细线便在空中划出一个圆锥面，这样的模型叫“圆锥摆”。圆锥摆是研究水平面内质点做匀速圆周运动动力学关系的典型特例。小球(可视为质点)质量为$m = 50kg$，细线$AC$长度为$L=\frac{5}{3}m$，取重力加速度$g = 10m/s^{2}$。
(1)在紧贴着小球运动的水平面上加一光滑平板，使球在板上做匀速圆周运动，此时细线与竖直方向所成夹角为$\theta = 53^{\circ}$，如图丙所示，当小球的角速度$\omega$大于某一值$\omega_{1}$时，小球将脱离平板，则$\omega_{1}$为多大？
(2)如果撤去光滑平板，让小球在空中旋转，再用一根细线，同样一端系在该小球上，另一端固定在细杆上的$B$点，且当两条细线均伸直时，如图丁所示，各部分长度之比$\vert AB\vert:\vert AC\vert:\vert BC\vert = 5:3:4$。当小球以$\omega_{2}=\frac{2\sqrt{10}}{3}rad/s$匀速转动时，两细线对小球的拉力大小分别多大？
(3)在(2)情境下，若每根绳子能够承受的最大张力为$2500N$，则小球转动的最大角速度$\omega_{3}$不能超过多少？

答案： 分析与解
(1)当平板对小球支持力为$0$时，小球恰好脱离平板，此时重力和绳子拉力的合力提供向心力，根据牛顿第二定律，有
$mg\tan\theta = m\omega_{1}^{2}L\sin\theta$，
解得$\omega_{1}=\sqrt{\frac{g}{L\cos\theta}}=\sqrt{10}rad/s$。
(2)因为$\vert AB\vert:\vert AC\vert:\vert BC\vert = 5:3:4$，细线均伸直时细线与竖直方向所成夹角为$\alpha = 53^{\circ}$，又$\omega_{2}=\frac{2\sqrt{10}}{3}rad/s\lt\omega_{1}$，所以$BC$绳子处于松弛状态不可能伸直，即$T_{BC}=0$，设此时$AC$绳子与竖直方向的夹角为$\theta_{1}$，由平衡条件和牛顿第二定律，有
$T_{AC}\cos\theta_{1}=mg$，$T_{AC}\sin\theta_{1}=m\omega_{2}^{2}L\sin\theta_{1}$，
解得$T_{AC}=\frac{10000}{27}N$。
(3)$AC$绳的拉力大于$BC$绳的拉力，所以$AC$绳的拉力$T'_{AC}$先达到$2500N$，此时有
$T'_{AC}\sin53^{\circ}+T'_{BC}\sin37^{\circ}=m\omega_{3}^{2}L\sin53^{\circ}$，
$T'_{AC}\cos53^{\circ}=T'_{BC}\cos37^{\circ}+mg$，
解得$\omega_{3}=\frac{\sqrt{165}}{2}rad/s$。
答案
(1)$\omega_{1}=\sqrt{10}rad/s$
(2)$T_{AC}=\frac{10000}{27}N$，$T_{BC}=0$
(3)$\omega_{3}=\frac{\sqrt{165}}{2}rad/s$