2025年小题狂做高中物理必修第二册人教版巅峰版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中物理必修第二册人教版巅峰版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.(多选,2025 湖南长郡二十校联盟模拟)如图甲所示,轻杆一端与一小球相连,另一端连在光滑固定轴上,可在竖直平面内自由转动. 现使小球在竖直平面内做圆周运动,到达某一位置开始计时,取水平向右为正方向,小球的水平分速度 $v_x$ 随时间 $t$ 的变化关系如图乙所示. 不计空气阻力. 下列说法中正确的是
(
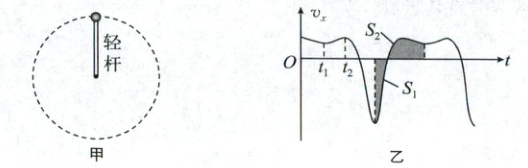
A.$t_1$ 时刻小球通过最高点,图乙中 $S_1$ 和 $S_2$ 的面积不相等
B.$t_2$ 时刻小球通过最高点,图乙中 $S_1$ 和 $S_2$ 的面积相等
C.$t_1$ 时刻的杆中弹力一定大于 $t_2$ 时刻的杆中弹力
D.在小球做一次完整圆周运动的过程中,杆中弹力一定两次为零
(
CD
)
A.$t_1$ 时刻小球通过最高点,图乙中 $S_1$ 和 $S_2$ 的面积不相等
B.$t_2$ 时刻小球通过最高点,图乙中 $S_1$ 和 $S_2$ 的面积相等
C.$t_1$ 时刻的杆中弹力一定大于 $t_2$ 时刻的杆中弹力
D.在小球做一次完整圆周运动的过程中,杆中弹力一定两次为零
答案:
1. CD 由题图可知,图像关于$t_1$时刻对称,故$t_1$时刻小球通过最高点,面积$S_1$表示的是小球从最低点运动到水平直径最左端位置的过程中通过的水平位移大小,等于半径,$S_2$表示的是从水平直径最左端位置运动到最高点的过程中通过的水平位移大小,也等于半径,故A、B错误;由图可知,小球从$t_1$时刻开始运动到第一次与圆心等高位置过程中,水平方向的速度先增大后减小,故在$t_1$时刻轻杆对小球的弹力为支持力,而$t_2$时刻小球水平方向的速度最大,故$t_2$时刻杆对小球无弹力,故C正确;由以上的分析可知,小球通过最高点时杆对小球的弹力为支持力,在接下来的四分之一圆周上,杆对小球的弹力先是支持力后来变为拉力,一定存在一个杆对小球的弹力为零的位置,该位置关于过圆心的竖直线对称的位置弹力也为零,故在小球做一次完整圆周动的过程中,杆中弹力一定两次为零,故D正确。
2.(2024 河南周口月考)如图甲所示,质量均为 $m$ 的两个物块 $A$、$B$ 用不可伸长的轻绳相连,放在水平转盘上,初始状态绳子松弛. 已知两物块与转盘之间的动摩擦因数均为 $\mu$,最大静摩擦力等于滑动摩擦力,重力加速度大小为 $g$. 现让转盘由静止缓慢增加转速. 两物块所受摩擦力随角速度平方的变化图像如图乙所示,取摩擦力由 $B$ 指向 $A$ 为正方向,下列说法
(
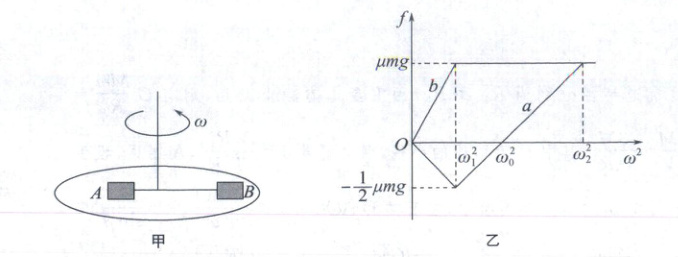
A.乙图中 $b$ 对应 $B$ 物块所受摩擦力随角速度平方的变化图像
B.$A$、$B$ 两物块到转盘圆心的距离之比为 $1:2$
C.$\omega^2_1:\omega^2_0:\omega^2_2 = 1:2:4$
D.当 $\omega = \omega_2$ 时,绳子的张力大小为 $2\mu mg$
错
误
的是(
D
)
A.乙图中 $b$ 对应 $B$ 物块所受摩擦力随角速度平方的变化图像
B.$A$、$B$ 两物块到转盘圆心的距离之比为 $1:2$
C.$\omega^2_1:\omega^2_0:\omega^2_2 = 1:2:4$
D.当 $\omega = \omega_2$ 时,绳子的张力大小为 $2\mu mg$
答案:
2. D 转盘开始由静止缓慢加速转动,A、B两物块靠静摩擦力提供向心力,开始时A、D两物块所受摩擦力均指向圆心,由题图乙可知,$b$图像为B物块所受摩擦力随角速度平方的变化图像,故A正确;当B物块达到最大静摩擦力时,有$\mu mg = m\omega_{B}^{2}r_{B}$,此时对A物块,有$\frac{1}{2}\mu mg = m\omega_{A}^{2}r_{A}$,联立上述两式解得$r_{B} = 2r_{A}$,$\omega_{1}^{2} = \frac{\mu g}{r_{B}}$,故B正确;设当角速度为$\omega_0$、$\omega_2$时绳子拉力分别为$T_0$、$T_2$,A物块做圆周运动的半径为$r$,则B物块做圆周运动的半径为$2r$,当$\omega = \omega_0$时,对B物块,有$T_0 + \mu mg = m\omega_{0}^{2} · 2r$,对A物块,有$T_0 = m\omega_{0}^{2}r$,解得$\omega_{0}^{2} = \frac{\mu g}{r}$,当$\omega = \omega_2$时,对A物块,有$T_2 - \mu mg = m\omega_{2}^{2}r$,对B物块,有$T_2 + \mu mg = m\omega_{2}^{2} · 2r$,联立解得$\omega_{2}^{2} = \frac{2\mu g}{r}$,$T_2 = 3\mu mg$,可得$\omega_{0}^{2} : \omega_{2}^{2} : \omega_{2}^{2} = \frac{\mu g}{2r} : \frac{\mu g}{r} : \frac{2\mu g}{r} = 1 : 2 : 4$,故C正确,D错误。
查看更多完整答案,请扫码查看


