2025年小题狂做高中物理必修第二册人教版巅峰版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中物理必修第二册人教版巅峰版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
3.(2024 湖北武汉期中)水平转盘可以绕竖直轴 $O_1O_2$ 转动,半径 $R = 0.6 m$,转盘中心 $O_2$ 处有一个光滑小孔,用一根长 $L = 1.1 m$ 的细线穿过小孔,将质量分别为 $m_A = 0.2 kg$、$m_B = 0.5 kg$ 的小球 $A$ 和小物块 $B$ 连接,小物块 $B$ 放在水平转盘的边缘且与转盘保持相对静止,如图所示. 现让小球 $A$ 在水平面内做角速度 $\omega_A = 5 rad/s$ 的匀速圆周运动,小物块 $B$ 与水平转盘间的动摩擦因数 $\mu = 0.3$,取 $g = 10 m/s^2$.

(1)求 $O_2A$ 与竖直方向的夹角 $\theta$ 及细线上的拉力大小.
(2)小球 $A$ 运动的速度大小不变,现使水平转盘转动起来,要使小物块 $B$ 与水平转盘间保持相对静止,求水平转盘角速度 $\omega_B$ 的取值范围.(假设最大静摩擦力等于滑动摩擦力)

(1)求 $O_2A$ 与竖直方向的夹角 $\theta$ 及细线上的拉力大小.
(2)小球 $A$ 运动的速度大小不变,现使水平转盘转动起来,要使小物块 $B$ 与水平转盘间保持相对静止,求水平转盘角速度 $\omega_B$ 的取值范围.(假设最大静摩擦力等于滑动摩擦力)
答案:
3.
(1)对A受力分析,由平衡条件,可知$T = \frac{m_Ag}{\cos \theta}$,
由牛顿第二定律,得$m_Ag \tan \theta = m_A\omega^{2}r_A$,
其中$r_A = (L - R)\sin \theta$,
解得$\cos \theta = \frac{4}{5}$,$\theta = 37°$,$T = 2.5 \mathrm{N}$。
(2)当物块B受到的最大静摩擦力$f_{max}$指向圆心时,转盘角速度$\omega_1$最大,由牛顿第二定律,有$T + \mu m_Bg = m_B\omega_{1}^{2}R$,
解得$\omega_1 = \sqrt{\frac{40}{3}} \mathrm{rad/s}$。
当物块B受到的最大静摩擦力$f_{max}$背离圆心时,转盘角速度$\omega_2$最小,由牛顿第二定律,有$T - \mu m_Bg = m_B\omega_{2}^{2}R$,
解得$\omega_2 = \sqrt{\frac{10}{3}} \mathrm{rad/s}$,
综上所述,水平转盘角速度的范围为$\sqrt{\frac{10}{3}} \mathrm{rad/s} \leq \omega \leq \sqrt{\frac{40}{3}} \mathrm{rad/s}$。
(1)对A受力分析,由平衡条件,可知$T = \frac{m_Ag}{\cos \theta}$,
由牛顿第二定律,得$m_Ag \tan \theta = m_A\omega^{2}r_A$,
其中$r_A = (L - R)\sin \theta$,
解得$\cos \theta = \frac{4}{5}$,$\theta = 37°$,$T = 2.5 \mathrm{N}$。
(2)当物块B受到的最大静摩擦力$f_{max}$指向圆心时,转盘角速度$\omega_1$最大,由牛顿第二定律,有$T + \mu m_Bg = m_B\omega_{1}^{2}R$,
解得$\omega_1 = \sqrt{\frac{40}{3}} \mathrm{rad/s}$。
当物块B受到的最大静摩擦力$f_{max}$背离圆心时,转盘角速度$\omega_2$最小,由牛顿第二定律,有$T - \mu m_Bg = m_B\omega_{2}^{2}R$,
解得$\omega_2 = \sqrt{\frac{10}{3}} \mathrm{rad/s}$,
综上所述,水平转盘角速度的范围为$\sqrt{\frac{10}{3}} \mathrm{rad/s} \leq \omega \leq \sqrt{\frac{40}{3}} \mathrm{rad/s}$。
例 1 (2025 重庆乌江新高考协作体月考)2019 年 3 月 10 日,长征三号乙运载火箭将“中星 6C”通信卫星(记为卫星Ⅰ)送入地球同步轨道上,主要为我国、东南亚、澳洲和南太平洋岛国等地区提供通信与广播业务。在同平面内的圆轨道上有一颗中轨道卫星Ⅱ,它运动的每个周期内都有一段时间 t(t 未知)无法直接接收到卫星Ⅰ发出的电磁波信号,因为其轨道上总有一段区域没有被卫星Ⅰ发出的电磁波信号覆盖到,这段区域对应的圆心角为 2α。已知卫星Ⅰ对地球的张角为 2β,地球自转周期为 T₀,引力常量为 G,则根据题中条件,可求出 ( )
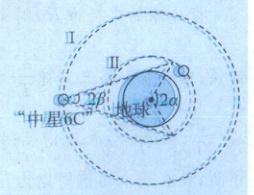
A.地球的平均密度为 $\frac{3π}{GT_{0}^{2}}$
B.卫星Ⅰ、Ⅱ的角速度之比为 $\frac{sin β}{sin(α - β)}$
C.卫星Ⅱ的周期为 $\sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}} · T_{0}$
D.题中时间 t 为 $\sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}} · \frac{α}{π}T_{0}$

A.地球的平均密度为 $\frac{3π}{GT_{0}^{2}}$
B.卫星Ⅰ、Ⅱ的角速度之比为 $\frac{sin β}{sin(α - β)}$
C.卫星Ⅱ的周期为 $\sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}} · T_{0}$
D.题中时间 t 为 $\sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}} · \frac{α}{π}T_{0}$
答案:
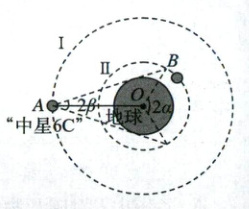
设卫星Ⅰ、Ⅱ的轨道半径分别为 R₁ 和 R₂,因卫星Ⅰ为静止卫星,则有 $G\frac{Mm}{R_{1}^{2}} = m\frac{4π^{2}}{T_{0}^{2}}R_{1}$,且有 $ρ = \frac{M}{V} = \frac{3M}{4πR^{3}}$,其中 R 为地球的半径,联立解得 $ρ = \frac{3πR_{1}^{3}}{GT_{0}^{2}R^{3}}$,A 错误;设卫星Ⅰ、Ⅱ的角速度分别为 ω₁ 和 ω₂,如图所示,在三角形 AOB 中,有 $\frac{AO}{sin(α - β)} = \frac{BO}{sin β}$,即 $\frac{R_{1}}{sin(α - β)} = \frac{R_{2}}{sin β}$,根据 $\frac{GMm}{r^{2}} = mω^{2}r$,可得 $ω = \sqrt{\frac{GM}{r^{3}}}$,故有 $\frac{ω_{1}}{ω_{2}} = \sqrt{(\frac{R_{2}}{R_{1}})^{3}}$,联立以上各式,有 $\frac{ω_{1}}{ω_{2}} = \sqrt{(\frac{R_{2}}{R_{1}})^{3}} = \sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}}$,B 错误;根据 $\frac{GMm}{r^{2}} = m(\frac{2π}{T})^{2}r$,可得 $T = 2π\sqrt{\frac{r^{3}}{GM}}$,因卫星Ⅰ为静止卫星,则其周期为 T₀,设卫星Ⅱ的周期为 T₂,则有 $\frac{T_{0}}{T_{2}} = \sqrt{(\frac{R_{1}}{R_{2}})^{3}} = \sqrt{\frac{sin^{3}(α - β)}{sin^{3}β}}$,整理得 $T_{2} = \sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}} · T_{0}$,C 正确;若卫星Ⅰ和卫星Ⅱ均不运动,卫星Ⅱ对应为圆心角为 2α,则有 $t = \frac{2α}{2π}T_{2} = \sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}} · \frac{α}{π}T_{0}$,但卫星之间是有相对运动,所以时间不可能为 $\sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}} · \frac{α}{π}T_{0}$,D 错误。
答案 C

设卫星Ⅰ、Ⅱ的轨道半径分别为 R₁ 和 R₂,因卫星Ⅰ为静止卫星,则有 $G\frac{Mm}{R_{1}^{2}} = m\frac{4π^{2}}{T_{0}^{2}}R_{1}$,且有 $ρ = \frac{M}{V} = \frac{3M}{4πR^{3}}$,其中 R 为地球的半径,联立解得 $ρ = \frac{3πR_{1}^{3}}{GT_{0}^{2}R^{3}}$,A 错误;设卫星Ⅰ、Ⅱ的角速度分别为 ω₁ 和 ω₂,如图所示,在三角形 AOB 中,有 $\frac{AO}{sin(α - β)} = \frac{BO}{sin β}$,即 $\frac{R_{1}}{sin(α - β)} = \frac{R_{2}}{sin β}$,根据 $\frac{GMm}{r^{2}} = mω^{2}r$,可得 $ω = \sqrt{\frac{GM}{r^{3}}}$,故有 $\frac{ω_{1}}{ω_{2}} = \sqrt{(\frac{R_{2}}{R_{1}})^{3}}$,联立以上各式,有 $\frac{ω_{1}}{ω_{2}} = \sqrt{(\frac{R_{2}}{R_{1}})^{3}} = \sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}}$,B 错误;根据 $\frac{GMm}{r^{2}} = m(\frac{2π}{T})^{2}r$,可得 $T = 2π\sqrt{\frac{r^{3}}{GM}}$,因卫星Ⅰ为静止卫星,则其周期为 T₀,设卫星Ⅱ的周期为 T₂,则有 $\frac{T_{0}}{T_{2}} = \sqrt{(\frac{R_{1}}{R_{2}})^{3}} = \sqrt{\frac{sin^{3}(α - β)}{sin^{3}β}}$,整理得 $T_{2} = \sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}} · T_{0}$,C 正确;若卫星Ⅰ和卫星Ⅱ均不运动,卫星Ⅱ对应为圆心角为 2α,则有 $t = \frac{2α}{2π}T_{2} = \sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}} · \frac{α}{π}T_{0}$,但卫星之间是有相对运动,所以时间不可能为 $\sqrt{\frac{sin^{3}β}{sin^{3}(α - β)}} · \frac{α}{π}T_{0}$,D 错误。
答案 C
查看更多完整答案,请扫码查看


