2025年小题狂做高中物理必修第二册人教版巅峰版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中物理必修第二册人教版巅峰版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.(2024 上海徐汇期中)如图所示,一劲度系数为 $ k $ 的轻质弹簧上端固定在天花板上,下端连接一质量为 $ m $ 的小球,已知弹簧受到的拉力 $ F = kx $,$ x $ 为其形变量。以小球的平衡位置 $ O $ 为坐标原点,$ x $ 轴正方向竖直向下。若取坐标原点为系统势能的零点,则当小球位于坐标为 $ x_0 $ 的位置时,系统的总势能为(
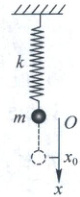
A.$ \frac{1}{2}kx_0^2 - mgx_0 $
B.$ \frac{1}{2}k(x_0 + \frac{mg}{k})^2 - mgx_0 $
C.$ \frac{1}{2}k(x_0 + \frac{mg}{k})^2 $
D.$ \frac{1}{2}kx_0^2 $
D
)
A.$ \frac{1}{2}kx_0^2 - mgx_0 $
B.$ \frac{1}{2}k(x_0 + \frac{mg}{k})^2 - mgx_0 $
C.$ \frac{1}{2}k(x_0 + \frac{mg}{k})^2 $
D.$ \frac{1}{2}kx_0^2 $
答案:
1. D 小球位于原点时,弹簧的弹力大小为$mg$,因为$F$与$x$成正比例关系,所以小球从原点到坐标为$x_0$的过程中,$F$对位移的平均值为$F = \frac{mg + (mg + kx_0)}{2} = mg + \frac{1}{2}kx_0$,根据功能关系,有$0 - E_p = mgx_0 - Fx_0$,解得$E_p = \frac{1}{2}kx_0^2$,故D正确。
2.(多选,2025 湖南常德七中开学考)如图所示,一根轻弹簧一端固定于 $ O $ 点,另一端与可视为质点的小滑块连接,把滑块放在倾角为 $ \theta = 30^{\circ} $ 的固定光滑斜面上的 $ A $ 点,此时弹簧恰好水平。将滑块从 $ A $ 点由静止释放,经 $ B $ 点到达位于 $ O $ 点正下方的 $ C $ 点。当滑块运动到 $ B $ 点时弹簧与斜面垂直,且此时弹簧恰好处于原长。已知 $ OB $ 的距离为 $ L $,弹簧始终在弹性限度内,重力加速度为 $ g $,则滑块由 $ A $ 运动到 $ C $ 的过程中(
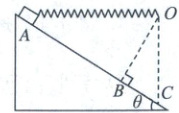
A.滑块的加速度先减小后增大
B.滑块的速度一直在增大
C.滑块经过 $ B $ 点时的速度大于 $ \sqrt{gL} $
D.滑块经过 $ C $ 点的速度可能小于 $ \sqrt{2gL} $
BC
)
A.滑块的加速度先减小后增大
B.滑块的速度一直在增大
C.滑块经过 $ B $ 点时的速度大于 $ \sqrt{gL} $
D.滑块经过 $ C $ 点的速度可能小于 $ \sqrt{2gL} $
答案:
2. BC 弹簧原长为$L$,在$A$点不离开斜面,则$k\left(\frac{L}{\sin 30^{\circ}} - L\right)\sin 30^{\circ} \leq mg\cos 30^{\circ}$,在$C$点不离开斜面,则有$k\left(\frac{L}{\cos 30^{\circ}} - L\right)\cos 30^{\circ} \leq mg\cos 30^{\circ}$,从$A$点滑至$C$点,设弹簧与斜面夹角为$\alpha$(范围为$30^{\circ} \leq \alpha \leq 90^{\circ}$),从$B$点滑至$C$点,设弹簧与斜面的夹角为$\beta$,则$mg\sin 30^{\circ} - kx\cos \beta = ma_2$,可知下滑过程中加速度一直沿斜面向下且减小,A错误,B正确;从$A$点滑到$B$点,由机械能守恒定律可得$mgL\cos 30^{\circ} + E_p = \frac{1}{2}mv_B^2$,解得$v_B = \sqrt{2gL\cos 30^{\circ} + 2\frac{E_p}{m}} = \sqrt{\sqrt{3}gL + 2\frac{E_p}{m}} > \sqrt{gL}$,C正确;从$A$点滑到$C$点,由机械能守恒可得$mg\frac{L}{\cos 30^{\circ}} + E_p' = \frac{1}{2}mv_C^2$,解得$v_C = \sqrt{2g\frac{L}{\cos 30^{\circ}} + 2\frac{E_p'}{m}} = \sqrt{\frac{4\sqrt{3}}{3}gL + 2\frac{E_p'}{m}} > \sqrt{2gL}$,D错误。
3.(2025 陕西西安模拟)如图所示,一质量为 $ m = 1\ kg $ 的长木板放置在光滑水平面上,木板的正中间放置一质量为 $ M = 3\ kg $ 的滑块,滑块与木板间的动摩擦因数为 $ \mu = 0.5 $。一条弹性绳一端系于天花板上的 $ O $ 点,另一端系于滑块中心,弹性绳的弹力与其伸长量满足胡克定律 $ F = kx $,劲度系数为 $ k = 100\ N/m $,弹性绳所具有的弹性势能 $ E_p = \frac{1}{2}kx^2 $。在 $ O $ 点正下方 $ A $ 点固定一光滑的圆环,弹性绳从环中穿过,已知 $ O $、$ A $ 之间距离与弹性绳原长相等,当滑块在 $ O $、$ A $ 的正下方 $ B $ 点时,弹性绳的伸长量为 $ h = 0.1\ m $。某时刻突然在 $ B $ 处给予两者一共同向右的速度 $ v $,在 此后的运动过程中,滑块都不会从木板上滑下。
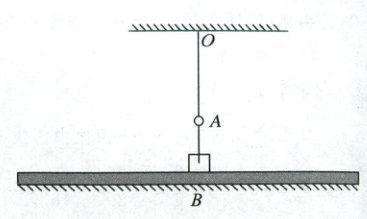
(1)$ v $ 为何值时,滑块到达某处时将与木板出现相对滑动,并求此位置与 $ B $ 的距离。
(2)若 $ v = 2\sqrt{3}\ m/s $,在刚好出现相对滑动时,使木板的速度瞬间变为 0 且固定不动,求此后滑块向右运动距 $ B $ 点的最大距离。
(3)求在第(2)问条件下滑块在木板上滑动因摩擦而产生的热量。

(1)$ v $ 为何值时,滑块到达某处时将与木板出现相对滑动,并求此位置与 $ B $ 的距离。
(2)若 $ v = 2\sqrt{3}\ m/s $,在刚好出现相对滑动时,使木板的速度瞬间变为 0 且固定不动,求此后滑块向右运动距 $ B $ 点的最大距离。
(3)求在第(2)问条件下滑块在木板上滑动因摩擦而产生的热量。
答案:
3.
(1) 当木板和滑块刚好出现相对运动时,滑块中心到$A$点的距离为$L$,位移为$x_1$,弹性绳的弹力大小为$F$,弹性绳与竖直方向的夹角为$\theta$,如图所示,弹性绳弹力的水平分力$F_x = kL\sin\theta = kx_1$,弹性绳弹力的竖直分力$F_y = kL\cos\theta = kh = 10 N$,对滑块,有$F_N + F_y = Mg$,对整体,有$F_x = (M + m)a$,对木板,有$f = ma$,又$f = \mu F_N = \mu(Mg - F_y) = 10 N$,联立求得$x_1 = 0.4 m$,即出现相对滑动的位置与$B$的距离为$0.4 m$。根据机械能守恒定律,有$\frac{1}{2}kL^2 - \frac{1}{2}kh^2 = \frac{1}{2}(m + M)v_1^2$,即$\frac{1}{2}kx_1^2 = \frac{1}{2}(m + M)v_1^2$,解得$v_1 = 2 m/s$,即$v > v_1 = 2 m/s$时滑块到达某处时将与木板出现相对滑动。

(2) 因为$v = 2\sqrt{3} m/s > 2 m/s$,设滑块和木板刚好出现相对滑动时的共同速度为$v_2$,根据机械能守恒定律,有$\frac{1}{2}kx_2^2 = \frac{1}{2}(m + M)v_2^2 - \frac{1}{2}(m + M)v^2$,其中$x_2 = x_1 = 0.4 m$,求得$v_2 = 2\sqrt{2} m/s$,此后木板停止运动,物块相对木板向右滑动,以向右为正方向,设滑块速度为零时相对$B$点的位移为$x_3$,根据能量守恒定律,有$\frac{1}{2}kx_3^2 - \frac{1}{2}kx_2^2 + f(x_3 - x_2) = \frac{1}{2}Mv_2^2$,解得$x_3 = 0.6 m$(另一解$x_3 = -0.8 m$不合理,舍去),故滑块向右运动距$B$点的最大距离为$0.6 m$。
(3) 因$kx_3 = 100 × 0.6 N = 60 N > f = 10 N$,故滑块不能静止而向左滑动。设向右为正方向,设滑块向左滑动直至速度再次为零时相对$B$点的位移为$x_4$,根据能量守恒定律,有$\frac{1}{2}kx_3^2 - \frac{1}{2}kx_4^2 = f(x_3 - x_4)$,解得$x_4 = -0.4 m$(另一解$x_4 = 0.6 m$不合理,舍去),负号说明滑块位于$B$点左侧$0.4 m$处,因$k\vert x_4\vert = 100 × 0.4 N = 40 N > f = 10 N$,故滑块不能静止而向右运动。同理对滑块再向右运动直至速度为零的过程,有$\frac{1}{2}kx_4^2 - \frac{1}{2}kx_5^2 = f(x_5 - x_4)$,解得$x_5 = 0.2 m$(另一解$x_5 = -0.4 m$不合理,舍去),因$kx_5 = 100 × 0.2 N = 20 N > f = 10 N$,故滑块不能静止而向左运动。同理,对滑块再向左运动直至速度为零的过程,有$\frac{1}{2}kx_5^2 - \frac{1}{2}kx_6^2 = f(x_5 - x_6)$,解得$x_6 = 0$(另一解$x_6 = 0.2 m$不合理,舍去),故滑块最终静止于$B$点。在木板固定不动直至滑块停止运动的整个过程中,设滑块与木板摩擦产生的热量为$Q$,根据能量守恒定律,有$Q = \frac{1}{2}kx_2^2 + \frac{1}{2}Mv_2^2 = 20 J$。
3.
(1) 当木板和滑块刚好出现相对运动时,滑块中心到$A$点的距离为$L$,位移为$x_1$,弹性绳的弹力大小为$F$,弹性绳与竖直方向的夹角为$\theta$,如图所示,弹性绳弹力的水平分力$F_x = kL\sin\theta = kx_1$,弹性绳弹力的竖直分力$F_y = kL\cos\theta = kh = 10 N$,对滑块,有$F_N + F_y = Mg$,对整体,有$F_x = (M + m)a$,对木板,有$f = ma$,又$f = \mu F_N = \mu(Mg - F_y) = 10 N$,联立求得$x_1 = 0.4 m$,即出现相对滑动的位置与$B$的距离为$0.4 m$。根据机械能守恒定律,有$\frac{1}{2}kL^2 - \frac{1}{2}kh^2 = \frac{1}{2}(m + M)v_1^2$,即$\frac{1}{2}kx_1^2 = \frac{1}{2}(m + M)v_1^2$,解得$v_1 = 2 m/s$,即$v > v_1 = 2 m/s$时滑块到达某处时将与木板出现相对滑动。

(2) 因为$v = 2\sqrt{3} m/s > 2 m/s$,设滑块和木板刚好出现相对滑动时的共同速度为$v_2$,根据机械能守恒定律,有$\frac{1}{2}kx_2^2 = \frac{1}{2}(m + M)v_2^2 - \frac{1}{2}(m + M)v^2$,其中$x_2 = x_1 = 0.4 m$,求得$v_2 = 2\sqrt{2} m/s$,此后木板停止运动,物块相对木板向右滑动,以向右为正方向,设滑块速度为零时相对$B$点的位移为$x_3$,根据能量守恒定律,有$\frac{1}{2}kx_3^2 - \frac{1}{2}kx_2^2 + f(x_3 - x_2) = \frac{1}{2}Mv_2^2$,解得$x_3 = 0.6 m$(另一解$x_3 = -0.8 m$不合理,舍去),故滑块向右运动距$B$点的最大距离为$0.6 m$。
(3) 因$kx_3 = 100 × 0.6 N = 60 N > f = 10 N$,故滑块不能静止而向左滑动。设向右为正方向,设滑块向左滑动直至速度再次为零时相对$B$点的位移为$x_4$,根据能量守恒定律,有$\frac{1}{2}kx_3^2 - \frac{1}{2}kx_4^2 = f(x_3 - x_4)$,解得$x_4 = -0.4 m$(另一解$x_4 = 0.6 m$不合理,舍去),负号说明滑块位于$B$点左侧$0.4 m$处,因$k\vert x_4\vert = 100 × 0.4 N = 40 N > f = 10 N$,故滑块不能静止而向右运动。同理对滑块再向右运动直至速度为零的过程,有$\frac{1}{2}kx_4^2 - \frac{1}{2}kx_5^2 = f(x_5 - x_4)$,解得$x_5 = 0.2 m$(另一解$x_5 = -0.4 m$不合理,舍去),因$kx_5 = 100 × 0.2 N = 20 N > f = 10 N$,故滑块不能静止而向左运动。同理,对滑块再向左运动直至速度为零的过程,有$\frac{1}{2}kx_5^2 - \frac{1}{2}kx_6^2 = f(x_5 - x_6)$,解得$x_6 = 0$(另一解$x_6 = 0.2 m$不合理,舍去),故滑块最终静止于$B$点。在木板固定不动直至滑块停止运动的整个过程中,设滑块与木板摩擦产生的热量为$Q$,根据能量守恒定律,有$Q = \frac{1}{2}kx_2^2 + \frac{1}{2}Mv_2^2 = 20 J$。
查看更多完整答案,请扫码查看


