《2025年小题狂做高中物理必修第二册人教版巅峰版》

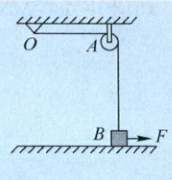
例 2（2024 江苏镇江期中）如图所示，一根轻质橡皮绳固定于 $ O $ 点，通过定滑轮 $ A $ 与质量为 $ m $ 的物块 $ B $ 相连接，物块 $ B $ 静止在 $ A $ 正下方的粗糙水平面上。$ O $、$ A $ 间距恰好为橡皮绳的原长，$ A $ 到物块的距离为 $ L $，现对物块施加一个水平向右的恒力 $ F = mg $，物块立刻获得 $ \frac{3}{4}g $ 的初始加速度开始向右运动，$ g $ 为重力加速度。物块与地面间的动摩擦因数 $ \mu = 0.5 $，橡皮绳产生的弹力满足胡克定律，物块 $ B $、定滑轮 $ A $ 可看作质点且不考虑其他摩擦。求：

（1）橡皮绳的劲度系数 $ k $。
（2）物块向右运动到与初始位置相距为 $ x $ 时，其加速度 $ a $ 与 $ x $ 的关系式。
（3）物块向右运动的最大速度 $ v_m $。

答案：
分析与解
（1）对 $ B $ 受力分析，由牛顿第二定律，有
$ F - f = ma $，
解得 $ f = F - ma = mg - \frac{3}{4}mg = \frac{1}{4}mg $。
又 $ f = \mu N $，
由于竖直方向的合力为 0，则
$ F' + N = mg $，
可得橡皮绳的弹力为
$ F' = \frac{1}{2}mg $，
根据胡克定律，有
$ F' = kL $，
解得 $ k = \frac{mg}{2L} $。
（2）物块向右运动到与初始位置相距为 $ x $ 时，设橡皮绳伸长量为 $ L_1 $，绳与水平方向的夹角为 $ \theta $，可得
$ f = \mu (mg - kL_1\sin\theta) $，
由牛顿第二定律，可得
$ F - f - kL_1\cos\theta = ma $，
由几何关系可得
$ L_1\cos\theta = x $，
$ L_1\sin\theta = L $，
联立解得 $ a = \frac{3}{4}g - \frac{g}{2L}x $ 或者 $ x = \frac{3}{2}L - \frac{2L}{g}a $。
（3）物块向右运动至最大速度时，加速度为 0，此时水平位移为
$ x = \frac{3}{2}L $，
橡皮绳弹力做的功为
$ W_{弹} = -\frac{0 + \frac{3}{4}mg}{2} · \frac{3}{2}L = -\frac{9}{16}mgL $，
摩擦力为定值，做的功为
$ W_f = -\frac{3}{8}mgL $，
由动能定理，可得
$ W_F + W_{弹} + W_f = \frac{1}{2}mv_m^2 - 0 $，
解得 $ v_m = \frac{3}{4}\sqrt{2gL} $。
另解：物块向右运动至最大速度时，加速度为 0，此时水平位移为
$ x = \frac{3}{2}L $，
由第（2）问可知 $ a - x $ 关系图像如图所示，由运动学公式，有

$ v^2 - v_0^2 = 2ax $，
可得 $ v_m^2 = 2\sum ax $，
其中 $ \sum ax $ 等于 $ a - x $ 图像中图线与 $ x $ 轴围成的面积，即
$ \sum ax = \frac{1}{2} × \frac{3}{4}g · \frac{3}{2}L = \frac{9}{16}gL $，
综合上述分析可得 $ v_m = \frac{3}{4}\sqrt{2gL} $。
答案（1）$ k = \frac{mg}{2L} $ （2）$ a = \frac{3}{4}g - \frac{g}{2L}x $ 或 $ x = \frac{3}{2}L - \frac{2L}{g}a $ （3）$ v_m = \frac{3}{4}\sqrt{2gL} $