《2025年小题狂做高中物理必修第二册人教版巅峰版》

例 2 (多选，2024 河北邢台期中)2020 年 1 月 7 日，在西昌卫星发射中心用“长征三号”运载火箭将通信技术试验卫星五号送入预定轨道，标志着我国航天卫星通信技术更加完善。在卫星之间传递信息时，有时会发生信号遮挡现象。如图所示，绕地球运行的通信卫星 a 和另一卫星 b 运行轨道在同一个平面内，绕行方向相同，但轨道半径不同，a 是地球同步卫星，能够直线覆盖地球的张角是 θ₁，b 是离地球较近的另一颗卫星，对地球的直线覆盖张角是 θ₂，且 $2sin\frac{θ_{1}}{2} = sin\frac{θ_{2}}{2}$。地球自转周期为 T₀，卫星 a 可以持续向卫星 b 发出信号(沿直线传播)，但由于 a、b 运行周期不同，每过一段时间，就会出现 a 发出的信号因地球遮挡，使卫星 b 接收不到信号而联系中断，则 ( )

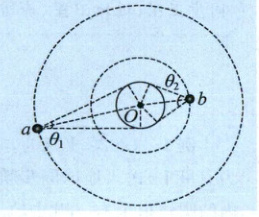
A.a、b 两卫星的轨道半径关系 $r_{a} = 4r_{b}$
B.卫星 b 的周期 $T_{b} = \frac{\sqrt{2}}{4}T_{0}$
C.卫星 b 的角速度 $ω_{b} = \frac{16π}{T_{0}}$
D.每次卫星 b 信号中断的时间是 $\frac{(θ_{1} + θ_{2})T_{0}}{2π(2\sqrt{2} - 1)}$

答案：
设地球的半径为 R，则 $sin\frac{θ_{1}}{2} = \frac{R}{r_{a}}$，$sin\frac{θ_{2}}{2} = \frac{R}{r_{b}}$，由 $2sin\frac{θ_{1}}{2} = sin\frac{θ_{2}}{2}$，解得 $r_{a} = 2r_{b}$，故 A 错误；由开普勒第三定律 $\frac{a^{3}}{T^{2}} = k$，有 $\frac{r_{a}^{3}}{T_{0}^{2}} = \frac{r_{b}^{3}}{T_{b}^{2}}$，解得 $T_{b} = \frac{\sqrt{2}}{4}T_{0}$，故 B 正确；卫星 b 的角速度 $ω_{b} = \frac{2π}{T_{b}} = \frac{4\sqrt{2}π}{T_{0}}$，故 C 错误；如图所示，由于地球遮挡 a、b 两卫星之间通信信号会周期性中断，设在一个通信周期内，a、b 两卫星通信中断的时间为 t，有 $(ω_{b} - ω_{a})t = 2α$，由几何关系知 $\frac{θ_{1}}{2} + \frac{θ_{2}}{2} = α$，解得 $t = \frac{(θ_{1} + θ_{2})T_{0}}{2π(2\sqrt{2} - 1)}$，故 D 正确。

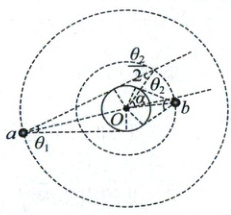
另解：本题 D 选项也可以用相对运动法来求解，即由几何知识可知，a、b 两卫星相对转过的角度为 θ₁ + θ₂，又两卫星转动方向相同，则相对角速度为 ωb - ωa，故中断通信的时间为 $t = \frac{θ_{1} + θ_{2}}{ω_{b} - ω_{a}} = \frac{(θ_{1} + θ_{2})T_{0}}{2π(2\sqrt{2} - 1)}$。
答案 BD