《2025年步步高精准讲练物理选择性必修第二册》

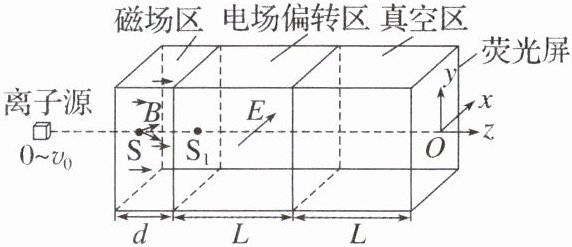
4. (14分)(2024·杭州市高二期末)如图所示，为某种离子诊断测量简化装置。离子源产生的离子从右侧狭缝射出后经加速器(图中未画出)加速后从小孔S进入与z轴平行的匀强磁场区。离子进入小孔S时速度方向均在yOz平面内且与z轴的夹角为θ(0≤θ≤α)。调节磁感应强度B的大小，可使部分离子通过小孔S₁进入电场强度沿x轴正方向、大小为E的电场偏转区，出偏转区后在真空区飞行直至打到荧光屏上，根据离子打在屏上的光点就可作出诊断。S、S₁、O点在同一水平线上，各区域沿z轴方向的长度分别为d、L、L，离子的质量m，电荷量+q，已知离子源可产生速率范围为0～v_0的离子，其中速率为v_0的离子经加速后，进入匀强磁场时的速率为v_m。离子的重力忽略不计。求：
(1)(3分)加速器中加速电压U的大小；
(2)(3分)若离子以v_m沿z轴方向进入小孔S，则其打在荧光屏上的x坐标值；
(3)(4分)若离子以v_m沿z轴方向进入小孔S，且电场E满足E=$\frac{2\sqrt{5}mv_m^2}{5qL}$，若要使该离子通过电场后打到荧光屏的O点，可以在真空区加沿y正方向的匀强磁场B'，则B'多大?
(4)(4分)从零开始增大磁感应强度B恰能使以速率v_m和偏角α入射的离子通过S₁进入电场，则所有通过S₁的离子在S点的速率v与偏角θ应满足的条件。

答案：
4.
(1)$\frac{m(v_{m}^{2} - v_{0}^{2})}{2q}$　
(2)$\frac{3qEL^{2}}{2mv_{m}^{2}}$　
(3)$\frac{\sqrt{5}mv_{m}}{qL}$　
(4)见解析
解析　
(1)在加速电场中，根据动能定理$qU = \frac{1}{2}mv_{m}^{2} - \frac{1}{2}mv_{0}^{2}$，解得$U = \frac{m(v_{m}^{2} - v_{0}^{2})}{2q}$。
(2)离子沿着$z$轴通过磁场区，通过电场偏转区的时间$t_{1} = \frac{L}{v_{m}}$，偏移量$x_{1} = \frac{1}{2}at_{1}^{2} = \frac{1}{2}\frac{qE}{m}(\frac{L}{v_{m}})^{2}$，由几何关系可得打在荧光屏上的$x$坐标值$x = 3x_{1} = \frac{3qEL^{2}}{2mv_{m}^{2}}$。
(3)如图所示，由类平抛运动可得$y = \frac{1}{2}at^{2} = \frac{1}{2}\frac{qE}{m}(\frac{L}{v_{m}})^{2} = \frac{\sqrt{5}}{5}L$，且$\tan\theta = \frac{2\sqrt{5}}{5}$，$AC = y\tan\theta = \frac{2}{5}L$，$BC = \sqrt{AB^{2} + AC^{2}} = \frac{3}{5}L$，$CD = BC$，故$C$为圆心$r = \frac{3}{5}L$，$v' = \frac{v_{m}}{\cos\theta} = \frac{3\sqrt{5}}{5}v_{m}$，根据洛伦兹力提供向心力$qv'B' = m\frac{v'^{2}}{r}$，解得$B' = \frac{\sqrt{5}mv_{m}}{qL}$。

(4)进入$S$的离子速率范围$\sqrt{v_{m}^{2} - v_{0}^{2}} \leq v \leq v_{m}$，$v$与$\theta$满足的条件为：①$0 ＜ \theta \leq \alpha$时，$nv\cos\theta = v_{m}\cos\alpha(n = 1,2,3·s)$，即$v = \frac{v_{m}\cos\alpha}{n\cos\theta}(n = 1,2,3·s)$；②$\theta = 0$时，所有离子均能通过$S_{1}$。