《2025年步步高精准讲练物理选择性必修第二册》

4. (多选)如图所示,虚线 MN 上方为匀强电场,下方为匀强磁场,匀强电场的电场强度大小为 E,方向竖直向下且与边界 MN 成 $\theta = 45°$ 角,匀强磁场的磁感应强度大小为 B,方向垂直纸面向外,在电场中有一点 P,P 点到边界 MN 的竖直距离为 d。现将一质量为 m、电荷量为 q 的带正电粒子从 P 处由静止释放(不计粒子所受重力,电场和磁场范围足够大)。则下列说法正确的是


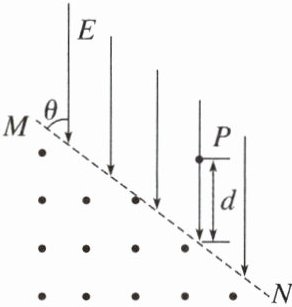
A.粒子第一次进入磁场时的速度大小 $v = \sqrt{\frac{2qEd}{m}}$
B.粒子第一次进入磁场到第一次离开磁场的时间 $t = \frac{3\pi m}{2qB}$
C.粒子第一次离开磁场到第二次进入磁场的时间 $t_1 = \sqrt{\frac{8qmd}{E}}$
D.粒子第一次在磁场中运动的半径 $R = \sqrt{\frac{2mEd}{qB}}$

答案： AB

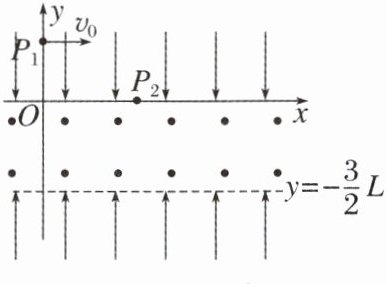
5. (12 分)如图所示,平面直角坐标系 xOy 中,在 x 轴上方和 $y = -\frac{3}{2}L$ 下方存在电场强度大小相等、方向相反(均平行于 y 轴)的匀强电场,在 x 轴下方和 $y = -\frac{3}{2}L$ 间存在垂直坐标平面向外的匀强磁场,一质量为 m、电荷量为 q 的带正电粒子,经过 y 轴上的点 $P_1(0,L)$ 时的速率为 $v_0$,方向沿 x 轴正方向,然后经过 x 轴上的点 $P_2(\frac{3}{2}L,0)$ 进入磁场,经偏转垂直 $y = -\frac{3}{2}L$ 虚线进入下方电场,不计粒子重力,$\sin 37° = \frac{3}{5}$,$\cos 37° = \frac{4}{5}$,求:
(1)(3 分)粒子到达 $P_2$ 点时的速度大小和方向
(2)(4 分)电场强度 E 和磁感应强度 B 的大小
(3)(5 分)粒子从 $P_1$ 点出发后至第 5 次经过 x 轴所经历的时间及此时经过 x 轴的位置坐标。

答案：
(1) 粒子在x轴上方电场中做类平抛运动，x方向匀速：$t_1=\frac{3L/2}{v_0}=\frac{3L}{2v_0}$。y方向匀加速：$L=\frac{0+v_y}{2}t_1$，得$v_y=\frac{4v_0}{3}$。合速度$v=\sqrt{v_0^2+v_y^2}=\frac{5v_0}{3}$，方向$\tan\theta=\frac{v_y}{v_0}=\frac{4}{3}$，$\theta=53°$（斜向下）。
答案：$\frac{5v_0}{3}$，与x轴正方向成$53°$角斜向下。
(2) 由$L=\frac{1}{2}at_1^2$，$a=\frac{qE}{m}$，得$E=\frac{8mv_0^2}{9qL}$。磁场中，半径$r=\frac{5L}{2}$，由$qvB=\frac{mv^2}{r}$，得$B=\frac{2mv_0}{3qL}$。
答案：$E=\frac{8mv_0^2}{9qL}$，$B=\frac{2mv_0}{3qL}$。
(3) 各阶段时间：$t_1=\frac{3L}{2v_0}$，磁场中$t_2=t_6=\frac{37\pi L}{120v_0}$，$t_4=t_8=\frac{143\pi L}{120v_0}$，电场往返$t_3=t_7=\frac{15L}{4v_0}$，上方电场$t_5=t_9=\frac{9L}{4v_0}$。总时间$t=t_1+2(t_2+t_3+t_4)+2t_5=\frac{27L}{2v_0}+\frac{3\pi L}{v_0}$。位置：$x=3L/2+4L+3L+4L+3L=\frac{31L}{2}$。
答案：时间$\frac{27L}{2v_0}+\frac{3\pi L}{v_0}$，位置$(\frac{31L}{2},0)$。